Literaturverzeichnis
Next: Beispielausdruck Up: Theorie und Praxis der Previous: Perspektiven
- Aar89
-
E. H. L. Aarts.
Simulated Annealing and Boltzmann machines.
John Wiley & Sohns Ltd., 1989.
- AD93
-
D. Abramson and H. Dang.
School timetables: A case study using simulated annealing.
In Applied Simulated Annealing, Lecture Notes in Economics and
Mathematical Systems, chapter 5, pages 104-124. Springer-Verlag, 1993.
- AG82
-
E.L. Allgover and K. Georg.
Predictor-corrector and simplicial methods for approximating fixed
points and zero points of nonlinear mappings.
In A. Bachem, M. Grtschel, and B.Korte, editors, Mathematical
Programming, The State of the Art, pages 15-57, Bonn, 1982.
- AKK98
-
Sanjeev Arora, David Karger, and Marek Karpinski.
Polynomial time approximation schemes for dense instances of
NP-hard problems.
In JcSS, 1998.
noch nicht erschienen.
- Ali95
-
F. Alizadeh.
Interior point methods in semidefinite programming with applications
to combinatorial optimization.
SIAM J. Optim., 5(1):13-51, 1995.
- Bat96
-
Roberto Battiti.
Reactive search: Toward self-tuning heuristics.
In V.J. Rayward-Smith, I.H. Osman, C.R. Reeves, and G.D. Smith,
editors, Modern Heuristic Search Methods, chapter 4, pages 61-83. John
Wiley and Sons Ltd., 1996.
- Bau97
-
N. Baumont.
Scheduling staff using mixed integer programming.
Europ. J. Operat. Res., 98, 1997.
- BF96
-
Piotr Berman and Toshiro Fujito.
On approximation properties of the independent set problem for degree
3 graphs.
In 37th IEEE FOCS, 1996.
- BGH97
-
R.N. Bailey, K.M. Garner, and M.F. Hobbs.
Using simulated annealing and genetic algorithms to solve staff
scheduling problems.
Asia-Pacific Journal of Operational Research, 14:27-43, 1997.
- BHM96
-
A. Bachem, W. Hochstttler, and M. Malich.
The simulated trading heuristic for solving vehicle routing problems.
Discrete Appl. Math., 65, 1996.
- Bin92
-
Ken Binmore.
Fun and games.
D.C. Heath and Company, Lexington, 1992.
- BJKW96
-
Edmund Burke, Kirk Jackson, Jeff Kingston, and Rupert Weare.
Automated timetabling: The state of the art.
http://www.asap.cs.nott.ac.uk, 1996.
- BK98
-
Piotr Berman and Marek Karpinski.
On some tighter inapproximability results, further improvements.
Technical Report TR98-065, Electronic Colloquium on Computational
Complexity (ECCC), 1998.
http://www.eccc.uni-trier.de/eccc.
- BKP97
-
Edmund K. Burke, J.H. Kingston, and P.A. Pepper.
A standart data format for timetabling instances.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 98-105, 1997.
- Blu98
-
Norbert Blum.
Theoretische Informatik.
Oldenbourg Verlag, München,Wien, 1998.
- BNW95
-
E. K. Burke, J. P. Newall, and R. F. Weare.
A memetic algorithm for university exam timetabling.
In 1st International Conference on the Practice and Theory of
Automated Timetabling (ICPTAT'95, Napier University, Edinburgh, UK, 30th Aug
- 1st Sept 1995), pages 496-503, 1995.
- Bro95
-
A. E. Brouwer.
Block designs.
In M. Graham, L. Grötschel, and L. Lovasz, editors, Handbook of
Combinatorics, volume 1, chapter 14, pages 693-746. Elsevier, 1995.
- Car
-
M. Carter.
Timetabling literature.
ftp://ftp.cs.nott.ac.uk/ttp.
- Cat98
-
Oliver Catoni.
Solving scheduling problems by simulated annealing.
SIAM J. Control Optim., 36(5):1539-1575, 1998.
- CCKV96
-
Michele Conforti, Gerard Cornuejols, Ajai Kapoor, and Krisina Vusovic.
Perfect matchings in balanced hypergraphs.
Combinatorica, 16(3):325-329, 1996.
- CdW89
-
N. Chahal and D. de Werra.
An interactive system for constructing timetables on a PC.
European Journal of Operational Research, 40:32-37, 1989.
- CG97
-
William H. Cunningham and James F. Geelen.
The optimal path-matching problem.
Combinatorica, 17(3):315-337, 1997.
- CK81
-
Vincent P. Crawford and Elsie Marie Knoer.
Job mathcing with heterogeneous firms and workers.
Econometrica, 49.2, March 1981.
- CK93
-
T. B. Cooper and J. H. Kingston.
The solution of real instances of the timetabling problem.
The Computer Journal, 36:645-653, 1993.
- CK95a
-
Tim B. Cooper and Jeffrey H. Kingston.
The complexity of timetable construction problems.
In Proceedings of the First International Conference on the
Practice and Theory of Automated Timetabling (ICPTAT '95), pages 511-522,
1995.
- CK95b
-
Tim B. Cooper and Jeffrey H. Kingston.
A program for constructing high school timetables.
In Proceedings of the First International Conference on the
Practice and Theory of Automated Timetabling (ICPTAT '95), pages 132-143,
1995.
- CL92
-
J. Csima and L.Lovasz.
A matching algorithms for regular bipartite graphs.
Discrete Applied Mathematics, 35:197-203, 1992.
- CLR96
-
Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest.
Introduction to Algorithms.
MIT electrical engeneering and computer science series. MIT Press,
1996.
- CO97
-
David Corne and John Ogden.
Evolutionary optimisation of methodist preaching timetables.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 321-323, 1997.
- Cor97
-
David Corne.
Tradeoffs and phase transitions in the interactions between exam
splitting, clash, near clash, and room capacity constraints.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 318-320, 1997.
- Cos94
-
D. Costa.
A tabu search algorithm for computing an operational timetable.
European Journal of Operational Research, 76:98-110, 1994.
- CR97
-
J.P. Caldeira and A.C. Rosa.
School timetabling using genetic search.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 115-122, 1997.
- CR98
-
Alberto Caprara and Romeo Rizzi.
Improving a family of approximation algorithms to edge color
multigraphs.
http://www.deis.unibo.it, 1998.
- CT92
-
M. W. Carter and C. A. Tovey.
When is the classroom assignment problem hard?
Operations Research, 40:28-39, 1992.
Supp. No. 1.
- Cur88
-
Inmaculata Jacinta Curiel.
Cooperative Games.
PhD thesis, Katholieke Universiteit van Nijmegen, 1988.
- Cur96
-
Inmaculata Jacinta Curiel.
Cooperative game theory and applications.
Curacao, 1996.
- Die96
-
Reinhardt Diestel.
Graphentheorie.
Springer, Berlin,Heidelberg,New York et al., 1996.
- Dou95
-
P. Douchet.
Hypergraphs.
In M. Graham, L. Grötschel, and L. Lovasz, editors, Handbook of
Combinatorics, volume 1, chapter 7, pages 381-433. Elsevier, 1995.
- Dow97
-
Kathryn A. Dowsland.
Off-the-peg or made-to-measure? timetabling and scheduling with SA
and TS.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 7-26, 1997.
- DS90
-
Gunter Dueck and Tobias Scheuer.
Threshold accepting: A general purpose optimisating algorithm
appearing superior to simulated annealing.
J. comp. physics, 90:161-175, 1990.
- dW71
-
D. de Werra.
Construction of school timetables by flow methods.
INFOR, 9:12-22, 1971.
- dW85
-
D. de Werra.
An introduction to timetabling.
European Journal of Operational Research, 19:151-162, 1985.
- dW95
-
D. de Werra.
Some combinatorial models for course scheduling.
In Proceedings of the First International Conference on the
Practice and Theory of Automated Timetabling (ICPTAT '95), pages 1-20,
1995.
- dW96
-
D. de Werra.
Extensions of coloring modells for scheduling purposes.
Europ. J. Operat. Res., 1996.
- dW97
-
D. de Werra.
Restricted coloring models for timetabling.
Discrete Math., 165/166:161-170, 1997.
- dWE96
-
D. de Werra and J. Eschler.
Open shop sheduling with some additional constraints.
Graphs and Combinatorics, 1996.
- dWM95
-
D. de Werra and N. V. R. Mahadev.
Preassignment requirements in chromatic scheduling.
ORWP 95/02, EPFL, 1995.
Submitted for publication.
- dWMP93
-
D. de Werra, N. V. R. Mahadev, and U. N. Peled.
Edge chromatic scheduling with simultaneity constraints.
SIAM Journal on Discrete Mathematics, 6:631-641, 1993.
- ECF97
-
Saleh Elmohamed, Paul Coddington, and Geoffrey Fox.
A comparision of annealing techniques for academic course scheduling.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 146-166, 1997.
- EdHH98
-
A.E. Eiben, J.K. Van der Hauw, and J.I. Van Hemert.
Graph coloring with adaptive evolutionary algorithms.
J. Heuristics, 4:25-46, 1998.
- EIS76
-
S. Even, A. Itai, and A. Shamir.
On the complexity of timetable and multicommodity flow problems.
SIAM Journal on Computing, 5:691-703, 1976.
- FMP96
-
Klaus Fischer, Jörg P. Müller, and Makus Pischel.
Cooperative transportation scheduling: an application domain for
DAI.
Technical report, DFKI GmbH Saarbrücken, 1996.
- Gal84
-
David Gale.
Equilibrium in discrete exchange economy with money.
Int. J. Game Theory, 13(1):61-64, 1984.
- GLS88
-
M. Grötschel, L. Lovasz, and A. Schrijver.
Geometric Algorithms and Combinatorial Optimization, chapter 9.
Springer, Berlin, 1988.
- Got63
-
C. C. Gotlieb.
The construction of class-teacher time-tables.
In Proc. IFIP Congress Munchen 1962, pages 73-77, 1963.
- GPS92
-
Lars Gislen, Carsten Peterson, and Bo Soderbarg.
Complex scheduling with potts neural networks.
Neural Computation, 4:805-831, 1992.
- GPU98
-
GPUntis98, 1998.
Messevorführung auf der C'Bit 98 Hannover.
- Hal93
-
Magnús M. Halldórsson.
A still better performance guarantee for approximate graph coloring.
Information processing Letters, 45:19-23, 1993.
- Has96
-
Johan Hastad.
Clique is hard to approximate within
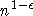 .
In 37th IEEE FOCS, 1996.
.
In 37th IEEE FOCS, 1996.
- Hax95
-
P.E. Haxel.
A condition for matchability in hypergraphs.
Graphs and Combinatorics, 1995.
- Hef97
-
A. Hefner.
A min-max theorem for a constraint matching problem.
Siam. J. Discrete Math., 10, 1997.
- Her92
-
A. Hertz.
Finding a feasible course schedule using tabu search.
Discrete Applied Mathematics, 35:225-270, 1992.
- HH93
-
R. Häggkvist and T. Hellgren.
Extensions of edge-colourings in hypergraphs I.
In Combinatorics, Paul Erdos is Eighty, volume 1 of
Mathematical Studies, pages 215-238. Bolai Society, Keszthely (Hungary),
1993.
- HHW96
-
Tad Hogg, Bernardo A. Huberman, and Colin P. Williams.
Phase transitions and the search problem.
Artificial Intelligence, 81:1-15, 1996.
- Hil81
-
A. J. W. Hilton.
School timetables.
Annals of Discrete Mathematics, 11:177-188, 1981.
- HK76
-
W. Hildenbrand and A.P. Kirman.
Introduction to Equilibrium Analysis.
Elsevier, Amsterdam, 1976.
- Hoc97
-
Dorit Hochbaum, editor.
Approximation algorithms for NP-hard problems.
PWS Publishing Company, Boston, 1997.
- Huc
-
A. Huck.
Mathematische Methoden des Operations-Research III.
Vorlesung, gehalten am Institut für Diskrete Mathematik WS 96/97.
- Jan97
-
Klaus Jansen.
The optimum cost chromatic partition problem.
In LNCS 1203. Springer, 1997.
- JT95
-
Tommy R. Jensen and Bjarne Toft.
Graph Coloring Problems.
John Wiley & Sons, New York, 1995.
- Jun86
-
W. Junginger.
Timetabling in germany - A survey.
Interfaces, 16:66-74, 1986.
- Jun90
-
Dieter Jungnickel.
Graphen, Netzwerke und Algorithmen.
BI-Wissenschaftsverlag, Mannheim, Wien, Zürich, 2 edition,
1990.
- KMSV94
-
Sanjeev Khanna, Rajeev Motwani, Madhu Sudan, and Umesh Vazirani.
On syntactic versus computational views of approximability.
In Proccedings of the 35th Annual IEEE Symposium on Foundations
of Computer Science, pages 819-830, 1994.
http://www.stanford.edu/people/motwani.
- Knu94
-
Donald E. Knuth.
The sandwich theorem.
The Electronic journal of Combinatorics, 1:#A1, 1994.
- KS96
-
Sanjeev Khanna and Madhu Sudan.
The optimisation complexity of constraint satisfaction problems.
Technical Report TR96-028, Electronic Colloquium on Computational
Complexity (ECCC), 1996.
http://www.eccc.uni-trier.de/eccc.
- Laj95
-
Gyuri Lajos.
Complete university modular timetabling using constraint logic
programming.
In Proceedings of the First International Conference on the
Practice and Theory of Automated Timetabling (ICPTAT '95), pages 364-375,
1995.
- Lec87
-
M. Leclerc.
Algorithmen für kombinatorische Optimierungsprobleme mit
Partitionsbeschränkungen.
PhD thesis, Universität Köln, 1987.
- Lew61
-
C. F. Lewis.
The School Time Table.
Cambridge University Press, 1961.
- Lio66
-
J. Lions.
Matrix reduction using the hungarian method for the generation of
school timetables.
Communications of the ACM, 9:349-354, 1966.
- LS95
-
R. Lindermeier and F. Siebert.
Softwareprüfung und Qualitätssicherung.
Oldenbourg Verlag, 1995.
- LY94
-
Carsten Lund and Mihalis Yannakakis.
On the hardness of approximation minimization problems.
J. ACM, 41(5):960-981, 1994.
- Mar98
-
Michael Marte.
Constraint-based grammar school timetabling: A case study, 1998.
Diplomarbeit Institut für Informatik TU München.
- Mic92
-
Zbigniew Michalewicz.
Genetic Algorithms + Data Structures = Evolution Programs.
Artificial Intelligence. Springer, 1992.
- Mim98
-
1998.
http://www.solnet.net/ mimosa.
- Miy98
-
Mitsunobu Miyake.
On the incentive properties of multi-item auctions.
Int. J. Game Theory, 27:1-19, 1998.
- MK98
-
H.H. Millar and M. Kiragu.
Cyclic and non-cyclic scheduling of 12h shift nurses by network
programming.
European Journal of operational research, 104(1998), 1998.
- MM96
-
Helmut E. Mausser and Michael J. Magazine.
Comparision of neural and heuristic methods for a timetabling
problem.
Europ. J. Operat. Res., 93:271-287, 1996.
- MR97
-
Nuno Mamede and Tiago Rente.
Repairing university timetables using genetic algorithms and
simulated annealing.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 187-204, 1997.
- MR98
-
Andrew J. Mason and David M. Ryan.
Integrated simulation, heuristic and optimistation approaches to
staff scheduling.
Op. Res., 46.2:161-175, 1998.
- PHB99
-
Jan Puzicha, Thomas Hofmann, and Joachim M. Buhmann.
Deterministic annealing: Fast physical heuristics for real-time
optimisation of large systems.
In Proceedings of the 15th IMACS World Conference on Scientific
Computation Modelling and Applied Mathematics, 1999?
noch nicht erschienen.
- PS89
-
Nicholas Pippenger and Joel Spencer.
Asymptotic behaviour of the chromatic index for hypergraphs.
J. Combinatorial Theory, A 51:24-42, 1989.
- Pul95
-
W.R. Pulleyblank.
Matchings and extensions.
In M. Graham, L. Grötschel, and L. Lovasz, editors, Handbook of
Combinatorics, volume 1, chapter 3, pages 179-233. Elsevier, 1995.
- Rei90
-
Karl Rüdiger Reischuk.
Einführung in die Komplexitätstheorie.
Teubner, Stuttgart, 1990.
- RF88
-
D.M. Ryan and J.C. Falkner.
On the integer properties of scheduling set partitioning models.
Europ. J. Operat. Res., 35:442-456, 1988.
- RHC97
-
Peter Ross, Emma Hart, and Dave Corne.
Some observations about GA-based exam timetabling.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 55-71, 1997.
- Rom82
-
Bernardo Prida Romero.
Examination scheduling in a large egineering school: a computer
assisted participative procedure.
Interfaces, 12(2):12-24, 1982.
- RW97
-
Vevek Ram and Peter Warren.
Automated timetable generation through distributed negotiation.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 345-346, 1997.
- SAW98
-
K. Steinhöfel, A. Abrecht, and C.K. Wong.
On various cooling schedules for simulated annealing applied to the
job shop problem.
In Michael Luby, Jose Rolim, and Maria Serna, editors,
Randomization and Approximation techniques in Computer Science, page 260ff.
Springer, 1998.
LNCS 1518.
- Sch94
-
Charles H. Schmauch.
ISO 9000 for Software Developers.
ASQC Quality Press, 1994.
- Sch95
-
Andrea Schaerf.
A survey of automated timetabling.
Technical Report CS-R9569, Centrum vor Wiskunde en Informatica, 1995.
- Sch96
-
A. Schaerf.
Tabu search techniques for large high-school timetabling problems.
CWI-Report CS-R9611, Centrum voor Wiskunde en Informatica, Amsterdam,
1996.
- Sed92
-
Robert Sedgewick.
Algorithmen.
Addison-Wesley, Bonn,Reading, 1992.
- Sli96
-
Tomaz Slivink.
Short proof of galvins theorem on the list-chromatic index of a
bipartite multigraph.
Combinatorics, Probability and Computing, 5:91-94, 1996.
- SM97
-
Pedro Suares and Nuno Mamede.
Micro-opportunistic timetabling.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), 1997.
- SS66
-
L.S. Shapley and M. Shubik.
Quasi-cores in a monetary economy with nonconvex preferences.
Econometrica, 34(4):805ff, 1966.
- SS78
-
L. A. Steen and J.A. Seebach.
Counterexamples in Topology.
Springer, New York, Heidelberg, 1978.
- SS79
-
G. Schmidt and T. Strohlein.
Timetable construction - an annotated bibliography.
The Computer Journal, 23:307-316, 1979.
- St97
-
Matthias Stüber.
Real world timetabling:a pragmatic view.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 258-267, 1997.
- Tuz97
-
Zsolt Tuza.
Graph colorings with local constraints a survey.
Discussiones Mathematicae Graph Theory, 17(2):161-228, 1997.
- VB96
-
L. Vandenberghe and S. Boyd.
Semidefinite programming.
SIAM Review, 38:49-95, 1996.
- Vyg
-
Jens Vygen.
Approximationsalgorithmen.
Vorlesung, gehalten am Institut für Diskrete Mathematik SS98.
Skript; Heausgabe im Rahmen eines Buches angekündigt.
- WK99
-
A. Wren and R. S. K. Kwan.
Installing an urban transport scheduling system.
J. of Scheduling, 2(1):3-19, 1999.
- Wre95
-
Anthony Wren.
Scheduling, timetabling and rostering - a special relationship?
In Proceedings of the First International Conference on the
Practice and Theory of Automated Timetabling (ICPTAT '95), pages 474-495,
1995.
- WW98
-
J. Wood and D. Whitaker.
Student centered school timetabling.
Journal of the Operational Research Society, 49:1146-1152,
1998.
- WZ97
-
George M. White and Junhan Zhang.
Generating complete university timetables by combining tabu search
with constraint logic.
In Proceedings of the second conference on practice and theory
of automated timetabling (PATAT), pages 268-277, 1997.
- ZG81
- W.I. Zangwill and C.B. Garcia. Equilibrium programming: The path following approach and dynamics. Mathematical Programming, 21:262-289, 1981.
(c) Martin Loehnertz 1999