Besonderheiten
Next: Sonstiges Up: Implementierung des Rahmenprogrammes Previous: Die interaktive Unterstützung
Besonderheiten
Integrität und kaskadierende Löschvorgänge
Die starke Abhängigkeit der Datenstrukturen voneinander und das Bestreben, daß durch das Löschen eines Objektes nicht die übrigen in Mitleidenschaft gezogen werden, führt zu dem Auftreten kaskadierender Löschvorgänge, wie sie aus dem Bereich relationaler Datenbanken bekannt sind. Zwei Mechanismen wurden vorgesehen, um dieses Problem zu behandeln:
- Eindeutige Schlüssel für alle auftretenden Datenobjekte (also auch Mengen und Gruppen): Dies ermöglicht es, einzelne Objekte zu löschen, ohne daß durch Indexverschiebungen Relationen verloren gehen. Eine normale Implementierung mit Zeigern ist hier ohnehin nur schwer möglich, da das Serialisierungskonzept von Visual C++ verlangt hätte, daß diese nach Speichern und Neuladen noch gültig sein müßten. Über die verwandten Hashs (vgl. Abschnitt 8.1) wird es zudem möglich, die Tatsache, daß ein Objekt gelöscht wurde, nachträglich festzustellen.
- Zeitmarken: Da das verwendete Visual C++ Framework aus diversen Aufrufen heraus überladene Update-Funktionen aufruft, war durch eine herkömmliche Kette von Funktionsaufrufen das Problem, alle Datensätze konsistent zu halten, nicht zu lösen, da entweder auf bereits gelöschte Objekte zurückgegriffen werden sollte oder aber unendliche Rekursionen auftraten. Daher beinhaltet jedes größere Konstrukt (d.h. das Mengensystem, Gruppensystem usw.) jeweils eine Zeitmarke, die die letzte Veränderung bezeichnet, und eine Marke, die angibt, wann zum letzten Mal ein Abgleich mit dem zugrundeliegenden System stattgefunden hat. Lediglich bei den Puffern kann eine Dirty-Marke verwendet werden. Vor jeder Operation kann so überprüft werden, ob sich an der eigenen Basis etwas geändert hat. Zeitmarke beschreibt hier nur einen Zähler, da die Zeit mit jeder Veränderung und nicht mit jeder Sekunde o.ä. inkrementiert wird. Die Verwendung entspricht aber der von Zeitmarken.
Objektbeziehungen
Wie oben bereits ausgeführt, umfassen die Objektbeziehungen auch die Beziehungen von Objekten zu Zeitstunden. Beziehungen zwischen Zeitstunden könnten auch eingegeben werden und die Angabe des Zeitablaufs ersetzen; sie werden aber nicht berücksichtigt, da dies den Benutzer wohl zu sehr verwirren würde.
Da nicht für jedes Objektpaar vom Benutzer ein eigener Wert angegeben werden kann, wurde ein System vorgesehen, nach dem
die Bewertungen von einer Menge auf ihre jeweiligen Untermengen übertragen wird. Dies ermöglicht z.B. Vorgaben
wie die, daß Rollstuhlfahrer am besten in Räumen mit Rampen unterrichtet werden (vgl. [BJKW96]). Als
Werte wurden 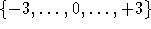 vorgesehen, wobei 0 andeuten soll, daß keine konkreten Vorlieben bestehen,
sondern der von den Obermengen her berechnete Wert eingesetzt werden soll.
Wesentliche Anforderungen an die so zu bestimmende Relation war, daß sie
vorgesehen, wobei 0 andeuten soll, daß keine konkreten Vorlieben bestehen,
sondern der von den Obermengen her berechnete Wert eingesetzt werden soll.
Wesentliche Anforderungen an die so zu bestimmende Relation war, daß sie
- symmetrisch und
- von der Reihenfolge der Berechnung unabhängig ist.
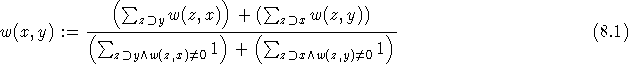
Hierbei bezeichnet 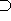 direkte Übermengen ohne Berücksichtigung der Mengen, die diese wiederum umfassen.
Damit ist es möglich, Vorgaben dieser indirekten Obermengen vollständig zu überstimmen. Bei der Bewertung bleiben
Obermengenbeziehungen mit dem Wert 0, d.h. unbestimmt unberücksichtigt, da die große Zahl der
Beziehungen dieses Typs ansonsten über Rundungsprozesse die vom Benutzer gewählten Eigenschaften völlig nivellieren würde.
Bei der Berechnung der einzelnen Werte wurde vorausgesetzt, daß der Graph der Obermengen- bzw. Untermengenrelation
azyklisch ist, was wie oben beschrieben sichergestellt wird.
direkte Übermengen ohne Berücksichtigung der Mengen, die diese wiederum umfassen.
Damit ist es möglich, Vorgaben dieser indirekten Obermengen vollständig zu überstimmen. Bei der Bewertung bleiben
Obermengenbeziehungen mit dem Wert 0, d.h. unbestimmt unberücksichtigt, da die große Zahl der
Beziehungen dieses Typs ansonsten über Rundungsprozesse die vom Benutzer gewählten Eigenschaften völlig nivellieren würde.
Bei der Berechnung der einzelnen Werte wurde vorausgesetzt, daß der Graph der Obermengen- bzw. Untermengenrelation
azyklisch ist, was wie oben beschrieben sichergestellt wird.
Zur Berechnung werden die einzelnen Mengen dem folgenden System unterworfen:
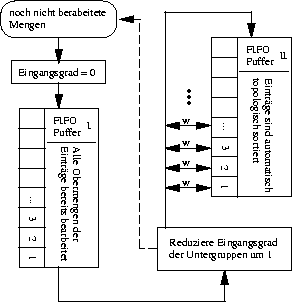
Die oben geforderten Eigenschaften ergeben sich unmittelbar aus der Formel. Diese setzt aber voraus, daß die entsprechenden Werte für die Übermengen bekannt sind: Es sei also angenommen, daß x neu in FIFO II aufgenommen werdon und seine Beziehung w zu einer Menge y aus FIFO II zu bestimmen ist.
- Die
Werte w(y,z) mit
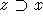 sind bekannt, da FIFO I topologisch sortiert ist und somit die Mengen
z bereits bearbeitet worden sein müssen, bevor x betrachtet wird.
sind bekannt, da FIFO I topologisch sortiert ist und somit die Mengen
z bereits bearbeitet worden sein müssen, bevor x betrachtet wird. - Die Werte w(z,x) mit
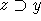 sind bekannt, da FIFO II die topologische Sortierung von
FIFO I übernommen hat und somit die Beziehung der Mengen z zu x geprüft wurde, bevor y betrachtet wird.
sind bekannt, da FIFO II die topologische Sortierung von
FIFO I übernommen hat und somit die Beziehung der Mengen z zu x geprüft wurde, bevor y betrachtet wird.
In einigen Versuchen zeigte sich, daß das Verhalten des Systems so am ehesten dem vom Benutzer erwarteten entspricht; dennoch verhält es sich in wenigen Fällen noch nicht der Intuition entsprechend, wie das folgende Beispiel illustriert: Seien a,b Teilmengen von A bzw. B. Die durch die dickeren Linien gekennzeichneten Relationen seien vom Benutzer vorgegeben.

Zunächst wird die gegebene Relation (A,B) auf (a,B) übertragen. An der Bestimmung des Wertes von (a,b) sind nun (A,b) und (a,B) gleichberechtigt beteiligt, was also - vorausgesetzt alle Werte sind ungleich Null - dazu führt, daß diese Relation als Wert den Mittelwert der beiden anderen erhält. Intuitiv würde man aber annehmen, sie müßte (A,b) erhalten, da dies (A,B), von dem (a,B) ja abstammt, überstimmt hat. Ein einfaches Bevorzugen der Benutzervorgaben an dieser Stelle erscheint aber ebenfalls nicht sinnvoll, da eine etwaige Beziehung (a,B') nicht neutralisiert werden dürfte.
Prüfung der Ressourcenzuteilung
Sind die Gruppen einmal Zeitpunkten zugewiesen, so kann mittels eines Matchings eine
optimale Ressourcenzuteilung vorgenommen werden. Hierzu wird ein bipartiter Graph gebildet, dessen eine Seite aus
sämtlichen Objekten und dessen andere Seite aus allen von den Gruppen gestellten Anforderungen besteht,
wobei für mehrfache Anforderungen entsprechend mehrere Knoten eingefügt werden:
Hierzu wird ein bipartiter Graph gebildet, dessen eine Seite aus
sämtlichen Objekten und dessen andere Seite aus allen von den Gruppen gestellten Anforderungen besteht,
wobei für mehrfache Anforderungen entsprechend mehrere Knoten eingefügt werden:
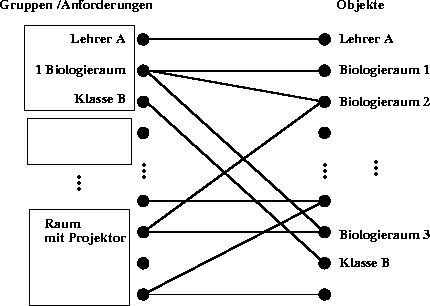
Der hierzu verwandte Ungarische Algorithmus ist im allgemeinen
mit einer Komplexität von 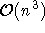 zu langsam, um interaktiv eingesetzt zu werden. Die Möglichkeit einer
solchen Zuordnung hingegen kann durch ungewichtetes Matching überprüft werden. Dies hat bereits eine prinzipiell
niedrigere Komplexität (
zu langsam, um interaktiv eingesetzt zu werden. Die Möglichkeit einer
solchen Zuordnung hingegen kann durch ungewichtetes Matching überprüft werden. Dies hat bereits eine prinzipiell
niedrigere Komplexität ( 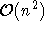 ), man kann den Vorgang aber noch weiter beschleunigen, da
der Algorithmus darauf beruht, bereits bestehende Matchings zu vergrößern. Die Tatsache, daß die Mengen im Schulbereich mit wenigen
Ausnahmen disjunkt sind, führt hier dazu, daß man mit einfachen Greedy-Verfahren Matchings erhalten kann, die nur wenige
Kanten weniger haben als ein maximales Matching. Bei im Test verwendeten ca. 40 Timeslots, also ebensovielen zu
berechnenden Matchings, fällt der Aufwand zu deren Berechnung gegenüber dem zur Erstellung der Ansicht nicht merklich ins Gewicht.
Wurden die entsprechenden Stunden automatisch erstellt, so kann ihr Bezug zu einer Stunde in den Voraussetzungen
leicht festgestellt werden. In diesem Fall wird die Voraussetzung und nicht die konkrete Menge für das Ressourcen-Matching verwandt,
so daß Vorschläge für die Verbesserung gemacht werden können. In der Implementierung sieht dies so aus, daß
Kollisionen, die auf diesem Wege aufgelöst werden können, anders angezeigt werden als solche, bei denen dies nicht der Fall ist.
), man kann den Vorgang aber noch weiter beschleunigen, da
der Algorithmus darauf beruht, bereits bestehende Matchings zu vergrößern. Die Tatsache, daß die Mengen im Schulbereich mit wenigen
Ausnahmen disjunkt sind, führt hier dazu, daß man mit einfachen Greedy-Verfahren Matchings erhalten kann, die nur wenige
Kanten weniger haben als ein maximales Matching. Bei im Test verwendeten ca. 40 Timeslots, also ebensovielen zu
berechnenden Matchings, fällt der Aufwand zu deren Berechnung gegenüber dem zur Erstellung der Ansicht nicht merklich ins Gewicht.
Wurden die entsprechenden Stunden automatisch erstellt, so kann ihr Bezug zu einer Stunde in den Voraussetzungen
leicht festgestellt werden. In diesem Fall wird die Voraussetzung und nicht die konkrete Menge für das Ressourcen-Matching verwandt,
so daß Vorschläge für die Verbesserung gemacht werden können. In der Implementierung sieht dies so aus, daß
Kollisionen, die auf diesem Wege aufgelöst werden können, anders angezeigt werden als solche, bei denen dies nicht der Fall ist.
Import und Export
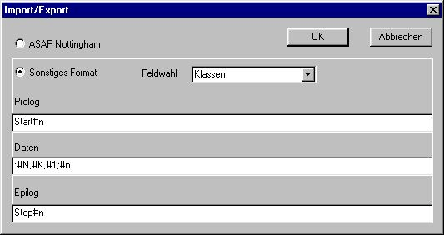
Da zahlreiche Schulen ihre Stundenplanvorgaben in der EDV erfaßt haben, schien die Implementierung einer flexiblen Import/Export - Funktion sinnvoll. Hierzu mußte dem Benutzer die Möglichkeit gegeben werden, ein eigenes Eingabeformat zu definieren. Da nicht anzunehmen ist, daß die auszutauschenden Datensätze eine allzu komplizierte Struktur aufweisen, wurde auf die Integration eines Parsergenerators verzichtet, und stattdessen eine einfache Wildcard - Substitution implementiert, die lediglich Ausdrücke der Form ab*c für Datensätze und a(bc*d)*e für Ressourcen-Gruppen zuläßt, was sogar eine Teilmenge der regulären Sprachen bleibt. Die Buchstaben stehen hier für Zeichenketten bestehend aus Feldbezeichnern (z.B. #N für Name etc.), einigen Makros (Dateiname, Datum, etc.) und beliebigen Zeichen. Gemäß dieser Schemata wird dann die Eingabedatei zerlegt bzw. die Ausgabe generiert. Eine Importmöglichkeit nach den Vorschlägen von BURKE [BKP97] wurde vorgesehen, aber nicht implementiert.
Das Einbinden von Lösungsverfahren
Um ein neues Lösungsverfahren einzubinden, muß dies lediglich als eine neue C++-Klasse erzeugt werden, die
von SolutionMethod abgeleitet ist. Im Konstruktor muß einmal die Funktion RegisterSolution mit
dem im Auswahlmenü anzuzeigenden Text als Argument aufgerufen werden. Und es muß mindestens ein Objekt dieser Klasse
erzeugt werden. Letzteres hat den Nachteil, daß jedes Lösungsverfahren den vom ihm benötigten Speicher erst bei Aufruf und
nicht schon im Konstruktor allokieren darf. Dies war aber dem expliziten Einbinden von Zeigern in die Klasse
SolutionMethod vorzuziehen. Die Erzeugung dieses Objektes muß in einer bestimmten Datei geschehen,
da die Lösungsverfahren in einer statischen Liste gespeichert werden, die von Visual C++ nicht zeitgleich mit
ihrer Klasse, sondern erst bei ihrer Definition initialisiert wird. Die einzige Möglichkeit in dieser Situation sicherzustellen,
daß dies vor der Initialisierung des ersten Verfahrens geschieht, ist die, diese Schritte in einer Quellcodedatei
zusammenzufassen.
Ein neues Lösungsverfahren sollte jeweils vier Funktionen überladen: Initialize, Step, ReadoutSolution und MakeClean,
wobei die Namen selbsterklärend sind.
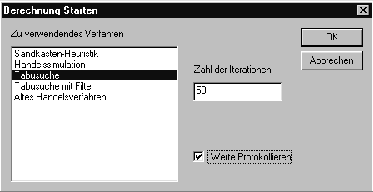
Die Klasse SolutionMethod stellt zusätzlich eine Funktion zur Verfügung, die es erlaubt, beliebige Ausdrücke in eine vorher vom Benutzer angegebene Datei zu schreiben. Dies, sowie die Möglichkeit zwischen den Verfahren zu wählen, dienen der Unterstützung einer einfacheren Evaluation verschiedener Verfahren.
Next: Sonstiges Up: Implementierung des Rahmenprogrammes Previous: Die interaktive Unterstützung (c) Martin Loehnertz 1999