Spieltheorie
Next: Ablauf der Auktion und Up: Verfahren 2: Handels - Previous: Erweiterung auf eine individuell
Spieltheorie
Terminologie
Bei dem gerade beschriebenen Prozeß handelte es sich um eine Situation bei der mehrere Objekte (Kunden) auf mehrere Händler (Fahrer) verteilt werden sollen. Um dieses Problem zu lösen, kommt es zu Kooperationen zwischen verschiedenen Gruppen von Fahrern (Knotenmenge eines Trading Matchings), bei der durch Zusammenarbeit ein in der Summe günstigeres Ergebnis entsteht. Dies führt sofort zu einigen zentralen Begriffen der Spieltheorie [Cur96], wobei an dieser Stelle eine Unterscheidung zwischen kooperativer und nichtkooperativer Theorie vorläufig nicht vorgenommen werden soll:
- Kooperatives Spiel
- Ein Kooperatives Spiel ist ein Paar <N,v> mit
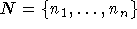 und
und 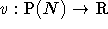 , wobei
N die Menge der Spieler ist und v eine Funktion, die jeder Teilmenge der Spieler den Gewinn zuordnet, den sie macht, wenn sich ihre
Mitglieder verbünden.
, wobei
N die Menge der Spieler ist und v eine Funktion, die jeder Teilmenge der Spieler den Gewinn zuordnet, den sie macht, wenn sich ihre
Mitglieder verbünden.
- Auszahlungsvektor
-
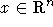 gibt an, wieviel von dem Gewinn einem einzelnen Spieler zugeordnet wird. Es sei für
gibt an, wieviel von dem Gewinn einem einzelnen Spieler zugeordnet wird. Es sei für 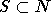
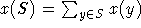 .
.
- Individuell rational
- verhalten sich die Spieler, wenn sie ein x mit
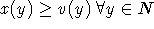 wählen.
wählen.
- Kern:
- Der Kern eines Spiels ist
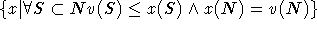 , d.h. die Menge der Auszahlungsvektoren, der gegenüber
keine Koalition eine Verbesserung erreichen kann.
, d.h. die Menge der Auszahlungsvektoren, der gegenüber
keine Koalition eine Verbesserung erreichen kann.
- Ökonomie mit unteilbaren Elementen
- Eine economy with indivisibilities ergänzt die Menge der Spieler
um eine endliche Menge von Objekten P, eine Startkonfiguration, die jedem Spieler einige der Objekte, sowie eine gewisse Menge Geld zuordnet, sowie
Relationen
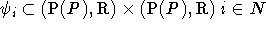 , die zu jedem Spieler angeben, ob ihm eine bestimmte Objekt-Geld-Kombination relativ zu einer anderen
mehr wert ist. Bei vielen gleichartigen Objekten werden diese häufig zu Vektoren zusammengefaßt. Die obigen Definitionen
übertragen sich entsprechend auf diese spezielle Form eines Spiels.
, die zu jedem Spieler angeben, ob ihm eine bestimmte Objekt-Geld-Kombination relativ zu einer anderen
mehr wert ist. Bei vielen gleichartigen Objekten werden diese häufig zu Vektoren zusammengefaßt. Die obigen Definitionen
übertragen sich entsprechend auf diese spezielle Form eines Spiels.
- Price Equilibrium
- Das Price Equilibrium beruht auf der Vorstellung, daß die Preise sämtlich exogen sind, d.h. daß die
Handlungen eines einzelnen Spielers irrelevant für die Preisbildung sind. Unter dieser Voraussetzung ist ein Price-Equilibrium\
ein Preisvektor p, der jedem Objekttyp einen Preis zuordnet und eine Verteilung der Waren, so daß der Markt leer (cleared) ist, d.h.
alle Ansprüche gesättigt sind. Für eine formale Definition siehe [Cur96].
Resultate
Ausgehend von den obigen Definitionen seien die für diese Anwendung zunächst wichtigsten Resultate genannt.
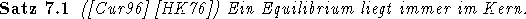
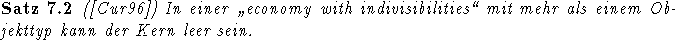
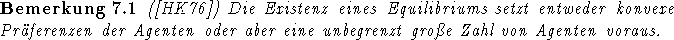
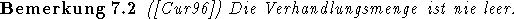
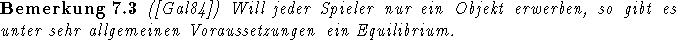
[HK76] führt zudem noch aus, daß selbst bei Existenz eines Equilibriums nicht gesichert ist, daß die Kräfte des Marktes das System gegen ein solches konvergieren lassen. Dieses Verhalten tritt nur in den z.B. in [Bin92] besprochen Fällen auf, in denen nur zwei Typen von Spielern vorkommen. Wie [SS66] zeigen, stellt sich mit wachsender Zahl von Händlern eine approximative Verbesserung der Situation in dem Sinne ein, daß die Gewinne durch Koalitionswechsel gegen Null konvergieren.
Reinterpretation im Rahmen der kombinatorischen Optimierung
Für den unmittelbaren Einsatz in der kombinatorischen Optimierung bringen diese allgemeinen Theorien von Spielen kaum Vorteile, da bereits
das Bestimmen von v(N) äquivalent zum Lösen des Problems ist, was sich auch darin äußert, daß einige andere spieltheoretische
Begriffe als Mittel über die Summe aller Permutationen der Spieler gebildet werden. Die von [Cur88] und [Cur96] gelösten
Spielprobleme mit bezug zur kombinatorischen Optimierung erweisen sich demzufolge auch allesamt als Repräsentationen von polynomiell
lösbaren Aufgaben, wie Matchings oder Spannbaumproblemen.
Die Nichtexistenz des Kerns bzw. eines kompetetiven Equilibriums oder eines konvergierenden Verfahrens ist dabei nicht so
hinderlich, wie es zunächst erscheint. Diese ist die Folge der Tatsache, daß sämtliche Teilnehmer bzw. der hier immer
präsente Beobachter, bereits vor Beginn des Spiels über all ihre Möglichkeiten informiert sind. Da die Menge der Objekte,
die des Geldes und die der Spieler begrenzt sind, müßte, da somit nur endlich viele Zustände gegeben sind, im Rahmen tatsächlicher Handelsvorgänge
ein Kreisen auftreten. Da aber nicht alle auf einem solchen Kreis beständig Gewinn machen würden, würde die Verweigerung eines
der Verlierer ausreichen, um das Kreisen zu stoppen. Dies steht nicht im Widerspruch zu den obigen Sätzen, da der blockierende Spieler bei
der reinen Vorüberlegung natürlich kein derartiges Vetorecht hätte, da er die entsprechenden Objekte/Gelder noch nicht besäße. Es
steht vielmehr im Einklang mit [HK76], die ausführen, daß das jeweilige Equilibrium nur im Sinne einer
vorher gegebenen Verteilung der Werte gegeben sein kann.
Beeindruckend ist die Allgemeinheit des Ergebnisses von GALE , allerdings
können die angegebenen Bedingungen nur als heuristische Hinweise dienen, da es in dem dort gegebenen Modell dennoch nicht
möglich ist, mehrere Spieler so aufeinander abzustimmen, daß sie in ihrer Gesamtheit so handeln wie ein einzelner.
, allerdings
können die angegebenen Bedingungen nur als heuristische Hinweise dienen, da es in dem dort gegebenen Modell dennoch nicht
möglich ist, mehrere Spieler so aufeinander abzustimmen, daß sie in ihrer Gesamtheit so handeln wie ein einzelner.
Fazit
Da sich somit ergibt, daß für den im Timetablingbetrachteten Fall mit einer großen, aber endlichen Zahl von Spielern,
einer endlichen Menge von Objekten und strikt nichtkonvexen Präferenzen weder die Existenz eines Equilibriums sicher ist,
geschweige denn die Konvergenz eines ökonomischen Prozesses gegen ein solches gezeigt werden kann, können die
Ergebnisse dieses Bereichs der Spieltheorie hier nur insoweit umgesetzt werden, als die Hoffnung bestehen kann, daß die Wahrscheinlichkeit einen stabilen Zustand zu erreichen, steigt, wenn man diejenigen
notwendigen Kriterien berücksichtigt, die bei einer konvexen, unendlichen oder speziellen Situation die Existenz von Equilibria sichert.
Ansonsten verbleibt nur das externe Steuern des Marktes. Hier gibt es
z.B. die Möglichkeit von Steuern, Abgaben oder aber auch die des direkten Eingriffs in die Zielfunktionen
der Händler. Eine Variante hierzu findet sich insbesondere beim Equilibrium Programming, bei dem das in
[HK76] geschilderte Verfahren durch eine externe Manipulation der Preise realisiert wird, wobei allerdings
streng konvexe Vorlieben der Spieler gefordert werden.
Eine andere Möglichkeit besteht darin, die Händler in ihren Möglichkeiten, und vor allem auch in ihrem
Wissen einzugrenzen. BINMOORE [Bin92] bezeichnet solche Situationen mit unwissenden
Spielern als Fälle von Bounded Rationality und zeigt auf, wie ein Spiel in solchen Situationen
konvergieren kann.
Der Rest dieses Abschnitts beschäftigt sich daher mit Experimenten zu eingeschränkten
Handelssituationen. Hierbei wird dennoch versucht eine Verbindung zur Spieltheorie aufrecht zu erhalten,
da, wenn man auf die Ausnutzung dieser Analogie verzichtet, die einzige Möglichkeit das Verfahren zu bewerten
in einer rein numerischen Überprüfung bestünde, wie sie auch bei BACHEM vorgenommen wird.
Next: Ablauf der Auktion und Up: Verfahren 2: Handels - Previous: Erweiterung auf eine individuell (c) Martin Loehnertz 1999