Das Prinzip des Simulated Trading
Next: Erweiterung auf eine individuell Up: Verfahren 2: Handels - Previous: Grundlagen
Das Prinzip des Simulated Trading
In diesem Kapitel soll zunächst der Rahmen der Problemstellung besprochen werden. Als Ausgangspunkt bietet sich hier das Verfahren von [BHM96] an, da diese Arbeit und die auf ihr aufbauenden Arbeiten [FMP96], die sich allerdings mehr mit dem dynamischen Fall beschäftigen, die bisher einzigen nachweisbaren Untersuchungen zu genau diesem Thema darstellen. Beide Arbeiten beschäftigen sich mit dem sog. Vehicle Routing-Problem, einer Erweiterung des Problems des Handlungsreisenden, in dem es darum geht, mehrere Punkte mit einer fest vorgegebenen Zahl von Routen zu überdecken, wobei je nachdem sowohl die benötigte Zeit als auch die gefahrene Gesamtstrecke zu berücksichtigen sind. Das klassische Problem ist die Versorgung mehrerer Kunden von einem zentralen Depot aus durch eine gegebene Zahl von Fahrzeugen.Basierend auf der Vorstellung, daß sich die Fahrer untereinander absprechen, schlägt [BHM96] folgende Heuristik vor: Jeder Fahrer bewertet seine Kunden nach dem zusätzlichen Aufwand, den sie für seine Tour bedeuten würden. Mit den entstandenen Verhältnissen als Basis für eine Wahrscheinlichkeitsverteilung wählt er dann zufällig einen der Kunden aus. Danach betrachten alle Fahrer die zum Verkauf stehenden Objekte und wählen mit einer Wahrscheinlichkeit, die durch die Differenz zwischen dem eingesparten Aufwand des Kollegen und dem Eigenen zusätzlichen Aufwand gegeben wird, ein Objekt zum Kauf aus.
Nun wird angenommen, daß alle diese Geschäfte tatsächlich möglich sind und auf Basis des potentiellen Ergebnisses wird der ganze Entscheidungsprozeß mehrere Schritte oft wiederholt. Jeder hierbei für möglich gehaltene Tauschvorgang wird dabei durch eine Kante in einem Graphen repräsentiert: Dieser besteht aus sovielen Levels, wie es Wiederholungen gegeben hat. Auf jedem Level repräsentieren die Knoten die Angebote bzw. Anfragen und die Kanten mögliche Handelsvorgänge.
Danach wird durch vollständige Enumerierung der Teilmengen der Kantenmenge des so erstandenen Graphen festgestellt, ob sogenannte Trading Matchings existieren und wenn ja, das mit maximalem Gewinn ausgewählt und umgesetzt. Hierbei unterscheidet sich dieses Trading Matching von einem herkömmlichen Matching insofern, als verlangt wird,
- daß jedes Objekt, das ein Händler verkauft, auch vorher von diesem besessen wurde,
- daß alle Handelsvorgänge, die der Händler auf einem niedrigeren Entscheidungslevel beantragt hat, ebenfalls stattgefunden haben, da sein Vorsatz, den Handel auf dem höheren Level\ durchzuführen, auf dieser Annahme beruht,
- daß einige problemspezifische Nebenbedingungen ebenfalls erfüllt sind,
Das Bestimmen eines optimalen Trading-Matchings ist, wie
in [BHM96] gezeigt wird,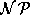 
-hart, es wird aber ausgesagt, daß die beteiligten Graphen so
wenige Kanten aufweisen, daß dies kein Problem darstellt. Im weiteren werden noch einige Vorschläge zur
dynamischen Parametervariation bzw. zum Einbetten in eine Tabusuche vorgebracht.
Läßt man die Anschauung weg, handelt es sich bei diesem Verfahren allerdings lediglich um eine heuristisch eingekleidete Variante von randomisiertem k-Opt
, da
eine bestimmte Anzahl von Objekten zufällig herausgegriffen und dann lokal optimal wiedereingesetzt wird. Es ist fraglich,
ob herkömmliches k-Opt, bei dem das Enumerieren vielleicht etwas länger dauern kann, das dafür aber alle Tauschvarianten
prüft, nicht effektiver wäre. So z.B. wird im Programm GPUntis
citeGPUntis deterministisches 3-Opt verwandt.
Next: Erweiterung auf eine individuell Up: Verfahren 2: Handels - Previous: Grundlagen (c) Martin Loehnertz 1999