Variationen des Graphenalgorithmus ohneTabusuche
Next: Zusammenfassung Up: Verfahren 1: Tabusuche Previous: Implementierung dieses Verfahrens
Variationen des Graphenalgorithmus ohne
Tabusuche
Wechsel der Reihenfolge mit Erinnerung
Der oben vorgeschlagene Algorithmus läßt Freiheiten bezüglich der Reihenfolge, in der die einzelnen Farben vergeben werden.
Hier besteht also die Möglichkeit, die Reihenfolge zu wählen. Da der Graphenalgorithmus kollidierende Stunden stets nur dann
setzt, wenn es sich nicht vermeiden läßt, treten Kollisionen immer erst später, d.h. bei
höheren Farbwerten, auf. Die Idee dieses Verfahrens besteht darin, den Algorithmus mehrmals laufen zu lassen
und dabei die Ergebnisse des letzten Durchlaufs, absteigend nach der Zahl der Kollisionen sortiert, als
Eingabe für die Parameterwahl zu verwenden, so daß die Kollisionen nun andere Zeiten betreffen. In Analogie zu dem Nivellieren eines
Sandhaufens durch Hin- und Herschieben wird dieses Verfahren im folgenden als Sandkasten-Heuristik beueichnet.
Rückschritte
Durch Bewertung normaler Kanten mit 1 und kritischer Kanten mit 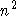 bzw.
bzw. 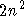 erhält man mit der Bewertung n eine
Möglichkeit, Kanten allen anderen vorzuziehen, ohne dabei die Korrektheit des Algorithmus zu gefährden (vgl. Abschnitt 6.6.5).
Es sei nun jeder Kante e des Multigraphen ein Wert
erhält man mit der Bewertung n eine
Möglichkeit, Kanten allen anderen vorzuziehen, ohne dabei die Korrektheit des Algorithmus zu gefährden (vgl. Abschnitt 6.6.5).
Es sei nun jeder Kante e des Multigraphen ein Wert 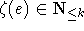 zugewiesen. Dieser Wert gibt an, zu welchem
Zeitpunkt der Berechnung das Gewicht einer Kante von 1 auf n wechseln soll. Der Wechsel auf
zugewiesen. Dieser Wert gibt an, zu welchem
Zeitpunkt der Berechnung das Gewicht einer Kante von 1 auf n wechseln soll. Der Wechsel auf 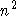 ist weiterhin
nur abhängig vom Knotengrad. Der Algorithmus basiert im wesentlichen auf der Beobachtung, daß beim UTP Kanten trotz
ausreichend kleinem Knotengrad nicht gesetzt werden können, da Kollisionen in den nicht repräsentierten Objekten auftreten können.
Deren Auftreten kann also hier nur nachträglich beobachtet werden. Der Algorithmus läuft wie folgt:
ist weiterhin
nur abhängig vom Knotengrad. Der Algorithmus basiert im wesentlichen auf der Beobachtung, daß beim UTP Kanten trotz
ausreichend kleinem Knotengrad nicht gesetzt werden können, da Kollisionen in den nicht repräsentierten Objekten auftreten können.
Deren Auftreten kann also hier nur nachträglich beobachtet werden. Der Algorithmus läuft wie folgt:
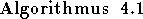
- Initialisiere alle
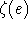 mit k
mit k - i:=0
- Berechne den i-ten Matchingschritt (s.o.)
- Hat eine Kante e des Matchings Wert n oder
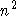 und kann wegen einer Kollision nicht gesetzt werden, und ist
und kann wegen einer Kollision nicht gesetzt werden, und ist 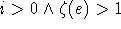
Setze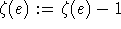 dann
dann 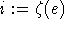 und gehe zu 3
und gehe zu 3 - Falls i<k: i=i+1 gehe zu 3
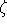 -Wert einer Kante reduziert werden muß, terminiert der Algorithmus offenbar nach spätestens
k*m Schritten.
-Wert einer Kante reduziert werden muß, terminiert der Algorithmus offenbar nach spätestens
k*m Schritten.
Next: Zusammenfassung Up: Verfahren 1: Tabusuche Previous: Implementierung dieses Verfahrens (c) Martin Loehnertz 1999