Implementierung dieses Verfahrens
Next: Variationen des Graphenalgorithmus ohneTabusuche Up: Verfahren 1: Tabusuche Previous: Hybridisierung mit einer Variante
Implementierung dieses Verfahrens
Die Tabuliste
Die Tabuliste wurde als Feld der Größe 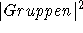 implementiert. Jeder Eintrag gibt an, bei der wievielten
Iteration das entsprechende Element in die Tabuliste eingetragen wurde. Dies ermöglicht es insbesondere, die
Länge der Tabuliste - auch zwischenzeitlich - beliebig zu wählen bzw. zu verändern. Die Tabulistenlänge wurde in diesem
ersten Versuch wegen der Größe des Lösungsraums so lang gewählt, daß gerade noch gesichert bleibt, daß stets ein
weiterer Schritt möglich ist. Hierzu sei s die Stundenzahl, G die Gruppenzahl und t die Zahl der Zeitstunden. z(x) sei die Stundenzahl
der Gruppe x. Dann ist die Zahl der möglichen Bewegungen gegeben durch:
implementiert. Jeder Eintrag gibt an, bei der wievielten
Iteration das entsprechende Element in die Tabuliste eingetragen wurde. Dies ermöglicht es insbesondere, die
Länge der Tabuliste - auch zwischenzeitlich - beliebig zu wählen bzw. zu verändern. Die Tabulistenlänge wurde in diesem
ersten Versuch wegen der Größe des Lösungsraums so lang gewählt, daß gerade noch gesichert bleibt, daß stets ein
weiterer Schritt möglich ist. Hierzu sei s die Stundenzahl, G die Gruppenzahl und t die Zahl der Zeitstunden. z(x) sei die Stundenzahl
der Gruppe x. Dann ist die Zahl der möglichen Bewegungen gegeben durch:
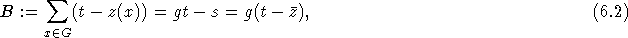
wobei 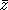 die durchschnittliche Stundenzahl einer Gruppe ist.
die durchschnittliche Stundenzahl einer Gruppe ist.
Mit jeder Eintragung in die Tabuliste wird die Anzahl der Möglichkeiten im Schnitt um 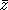 reduziert, wobei
außer acht gelassen wurde, daß damit eine bereits gesperrte Zeitstunde nochmals gesperrt werden kann.
Somit sollte die Tabuliste kürzer als
reduziert, wobei
außer acht gelassen wurde, daß damit eine bereits gesperrte Zeitstunde nochmals gesperrt werden kann.
Somit sollte die Tabuliste kürzer als 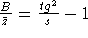 sein.
sein.
Der Filterschritt
Der Filterschritt besteht im wesentlichen darin, den Graphenalgorithmus dazu zu verwenden, die von der Tabusuche gewählte Konfiguration in eine solche umzuwandeln, die bezüglich der je zwei aus jeder Gruppe ausgewählten Elemente keine Kollisionen aufweist. Hierzu wird eine beliebige Reihenfolge der Zeitstunden gewählt und dann der Algorithmus angewandt. Hierbei werden im Gegensatz zum einfachen gewichteten Matching drei Klassen von Kanten betrachtet. Die oberste enthält die Kanten mit anliegenden Knoten kritischen Grades wie oben beschrieben. Die zweite Klasse enthält diejenigen Kanten, die von der Tabusuche für das betrachtete Zeitslot vorgesehen wurden. Die dritte beinhaltet all diejenigen Kanten, die für eine der bereits gesetzten Zeitstunden vorgeschlagen worden waren, aber nicht gesetzt werden konnten. Gibt es fest gesetzte Stunden, wird für diese eine Klasse 0 vorgesehen. Bei der Bestimmung werden die Kanten so gewichtet, daß jede Kante einer höheren Klasse Vorrang vor der Summe aller Kanten einer niedrigeren Klasse hat. Verzichtet man auf eine zusätzliche Gewichtung, so kann dieser Effekt dadurch erreicht werden, daß man zunächst ein Matching für Klasse 1 bestimmt, dieses dann zu einem von Klasse 2 erweitert, usw. Die Tatsache, daß bereits überdeckte Knoten überdeckt bleiben, sichert die Gültigkeit dieses Vorgehens. Dies wurde in der Form integriert, daß nur gegen Ende der Laufzeit eine Optimierung verlangt wird.
Startpunkt
Das Verfahren startet jeweils vom letzten gegebenen Stundenplan aus, wobei fehlende Stunden zufallsgesteuert hinzugefügt werden. Dies ermöglicht es einerseits, verschiedene andere Verfahren als Startpunktgeneratoren zu verwenden, andererseits können durch erneutes Starten der Tabusuche die Auswirkungen eines Löschens der Tabuliste untersucht werden.
Laufzeitanalyse
Mehr noch als bei genetischen Algorithmen ist eine Abschätzung der Konvergenzgeschwindigkeit der Tabusuche nahezu unmöglich.
Die einzige Möglichkeit, die es hier gibt, ist die geschickte Wahl der Aspiration-Funktion, die zumindest garantiert, daß das
Verfahren nicht langsamer ist als eine herkömmliche Abstiegsmethode.
Der Filterschritt hat wegen der Anwendung des
Ungarischen Algorithmus zur Prüfung der Ressourcenzuteilung eine Komplexität von 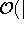 Objekte
Objekte  Zeitstunden|), wobei die Nachbearbeitung
hier vollkommen dominiert. Verwendet man dort ausschließlich das schnellere Matchingverfahren, so dominiert mit
Zeitstunden|), wobei die Nachbearbeitung
hier vollkommen dominiert. Verwendet man dort ausschließlich das schnellere Matchingverfahren, so dominiert mit
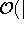 Lehrer
Lehrer  Zeitstunden|) Operationen das erste Matching.
Zeitstunden|) Operationen das erste Matching.
Next: Variationen des Graphenalgorithmus ohneTabusuche Up: Verfahren 1: Tabusuche Previous: Hybridisierung mit einer Variante (c) Martin Loehnertz 1999