Hybridisierung mit einer Variante des Algorithmus nach K¨ONIG
Next: Implementierung dieses Verfahrens Up: Verfahren 1: Tabusuche Previous: Wahl der Nachbarschaft
Hybridisierung mit einer Variante des Algorithmus nach K¨ONIG
Anwendungsvoraussetzungen
Da dieses Verfahren dem Algorithmus von K¨ONIG folgt, verlangt es die Vorgabe eines bipartiten Graphen. Dieser ist im RSTP im allgemeinen nicht gegeben, die Abweichungen sind aber insbesondere im Bereich der Sekundarstufe I häufig auf wenige Differenzierungsstunden beschränkt. Voraussetzung ist somit in erster Linie die folgende Bedingung:

Bei der konkreten Umwandlung des UTP wird aus jeder Gruppe je ein Element aus jeder Teilmenge ausgewählt. Eine Lösung
nach dem Satz von K¨ONIG garantiert also somit, daß bezüglich dieser Elemente keine Widersprüche auftreten können.
Im folgenden sei n die größere der beiden Knotenzahlen in dem so gewonnenen bipartiten Graphen und k die Zahl der Farben.
Des weiteren sei basierend auf obiger Bemerkung vereinbart:
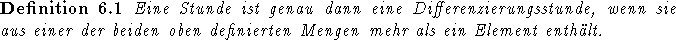
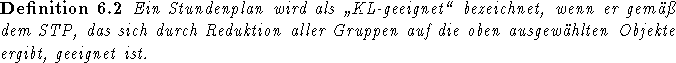
Die hiermit im Zusammenhang stehenden Überlegungen entspringen allerdings vollständig dem schulischen Kontext, da hier angenommen werden kann, daß Kollisionen in der im allgemeinen dritten Ressource Raum seltener sind und im Bereich von Schülern und Lehrern selten die Wahl zwischen verschiedenen Objekten möglich ist. Dies muß bei einer Universität oder Fachhochschule nicht mehr der Fall sein.
Gewichtetes Matching
Beim Algorithmus nach K¨ONIG (Satz 4.3) spielen Matchings, die alle Knoten maximalen
Grades überdecken, eine entscheidende Rolle (vgl. dort). Wie die Matchings abgesehen von dieser
Eigenschaft aussehen, ist für das Funktionieren des Algorithmus nicht von Bedeutung.
Es ist daher möglich, andere Kanten nach Belieben hinzuzunehmen. Ersetzt man nun das im Algorithmus nach K¨ONIG auftretende
einfache Matching durch gewichtetes Matching, so muß man lediglich dafür sorgen, daß stets alle Knoten maximalen Grades im zugehörigen Multigraphen
von den jeweiligen Matchings überdeckt werden. Sei hierzu im Graphen G=(V,E) von einer Gewichtung 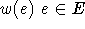 des Graphen ausgegangen,
die in irgendeiner Weise gewünschte Eigenschaften des Matchings kodiert. Sei A die Menge der Knoten mit maximalem Grad
und
des Graphen ausgegangen,
die in irgendeiner Weise gewünschte Eigenschaften des Matchings kodiert. Sei A die Menge der Knoten mit maximalem Grad
und 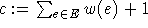 .
Dann definiere
.
Dann definiere 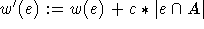 .
.
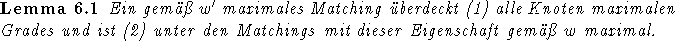
Beweis:
1. Satz 4.2 zeigt, daß es ein Matching gibt, das alle Knoten maximalen Grades überdeckt. Es genügt
also zu zeigen, daß jedes Matching mit dieser Eigenschaft gemäß w' schwerer ist als jedes andere, da damit das
schwerste Matching ingesamt eines von diesen sein muß. Ein Matching mit k<|A| überdeckten Knoten maximalen Grades hat
aber offenbar ein Gewicht von höchstens 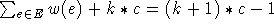 , während ein Matching mit |A| überdeckten
Kanten mindestens das Gewicht
, während ein Matching mit |A| überdeckten
Kanten mindestens das Gewicht 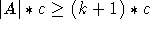 hat.
hat.
2. Da alle Matchings, die alle Knoten maximalen Grades überdecken, gleichviele dieser Knoten überdecken, gilt für
ein derartiges Matching stets w'(M)=w(M)+c*|A| und somit ist für diese 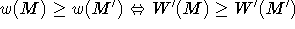 .
.
Eine ähnliche Idee findet sich in [CdW89], wobei diese Autoren die Gewichtungsmöglichkeit ausschließlich zur Erzwingung
der gewünschten Überdeckung von Knoten maximalen Grades verwenden , aber nicht explizit auf
die Garantien eingehen. Des weiteren finden sich ähnliche Überlegungen in [dW71]. Eine Frage, die sich an dieser
Stelle ebenfalls stellt, ist, ob alle Kanten um einen solchen, die übrige Bewertung dominierenden Betrag vergrößert werden sollten,
um stets maximale Matchings maximalen Gewichts zu erhalten. Auch wenn dies im Sinne der harten Nebenbedingungen sinnvoll wäre, wurde hier
davon abgesehen, da hiervon insbesondere die Nichtverfügbarkeiten betroffen würden, die zumeist ähnlich wichtig sind.
, aber nicht explizit auf
die Garantien eingehen. Des weiteren finden sich ähnliche Überlegungen in [dW71]. Eine Frage, die sich an dieser
Stelle ebenfalls stellt, ist, ob alle Kanten um einen solchen, die übrige Bewertung dominierenden Betrag vergrößert werden sollten,
um stets maximale Matchings maximalen Gewichts zu erhalten. Auch wenn dies im Sinne der harten Nebenbedingungen sinnvoll wäre, wurde hier
davon abgesehen, da hiervon insbesondere die Nichtverfügbarkeiten betroffen würden, die zumeist ähnlich wichtig sind.
Zur Gewichtung können nun mehrere Kriterien herangezogen werden:
- Die Tatsache, ob für ein Objekt die Zahl der noch zu setzenden Stunden gleich der Zahl der noch verbleibenden Stunden ist. Dieses Kriterium ist nicht hinreichend für eine Lösbarkeit des RSTP, da nicht berücksichtigt wird, ob sich diese Stunden auch tatsächlich plazieren lassen.
- Analog bei flexiblen Ressourcen, ob die Zahl der noch zu benutzenden Objekte gleich der Objektzahl multipliziert mit der Zahl der verbleibenden Zeitstunden ist.
- Die Tatsache, daß die entsprechende Stunde tight nach den Kriterien von GOTTLIEB ist, was eine Verbesserung im obigen Sinne darstellt, aber auch nicht hinreichend ist.
- Werte, die repräsentieren, wie weit die Stunde noch von den gerade beschriebenen Tatsachen entfernt ist, das heißt zum Beispiel, um wieviel die Zahl der verbleibenden Stunden größer ist, als die der benötigten. Dies führt zu einer Art Lookahead.
- Die zeitbezogenen Anforderungen bzw. Wünsche der Objekte.
- Relative Nebenbedingungen, sofern bereits andere Stunden gesetzt wurden.
Für die Hybridisierung günstige Eigenschaften
Auch mit einigen Modifikationen läßt sich dieses Verfahren, das lange Zeit das einzige polynomielle des gesamten
Gebietes war, nicht dazu verwenden, kompliziertere Zielfunktionen zu verfolgen bzw. Differenzierungen und Raumzuteilungen
zufriedenstellend zu lösen. Es hat aber, und aus diesem Grunde wurde es dem Verfahren nach GALVIN vorgezogen, die
Eigenschaft, eine in der Bewertungsmatrix kodierte gültige Färbung zu erhalten: Die Lehrer-Klassen-Kanten
(oder eine Auswahl derselben beim RSTP) müssen bei einer gültigen Lösung zu jeder Zeitstunde ein Matching bilden, das alle Knoten
kritischen Grades überdeckt. Versieht man also
in einem entsprechenden gewichteten Graphen diese Kanten mit dem Gewicht 1 und wertet die andern mit 0, so wird der
obige Algorithmus ein Matching finden, das diese Kanten verwendet. Faßt man also den
Algorithmus als eine Funktion 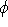 auf, die aus dem
auf, die aus dem 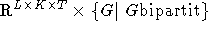 in die Menge S der KL-geeigneten Stundenpläne über G führt, so ist diese
surjektiv, da man jeden Zielpunkt erreichen kann, indem man ihn in die Eingabe 0,1-kodiert. Sei
in die Menge S der KL-geeigneten Stundenpläne über G führt, so ist diese
surjektiv, da man jeden Zielpunkt erreichen kann, indem man ihn in die Eingabe 0,1-kodiert. Sei 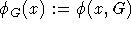 . Damit könnte der Algorithmus also
als Postoptimizer für beliebige andere Verfahren verwandt werden.
. Damit könnte der Algorithmus also
als Postoptimizer für beliebige andere Verfahren verwandt werden.
Andererseits erlaubt es dies aber auch, diesen Algorithmus als Bestandteil einer komplexeren Zielfunktion zu sehen.
Mit einer gegebenen Bewertung 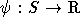 erhält man durch
erhält man durch 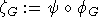 eine Abbildung von
eine Abbildung von
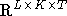 nach
nach 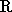 . Nimmt man G als fest an, so erhält man also eine
Optimierungsaufgabe der Form:
. Nimmt man G als fest an, so erhält man also eine
Optimierungsaufgabe der Form:
Finde 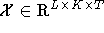 , so daß
, so daß 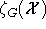 maximal wird. Im folgenden sollen die Auswirkungen dieser
Veränderung diskutiert werden.
maximal wird. Im folgenden sollen die Auswirkungen dieser
Veränderung diskutiert werden.
Auswirkungen der Hybridisierung
Häufig wird in der Literatur zum Timetabling angegeben [Dow97], daß die Oberfläche der Zielfunktionen
durch steile, schmale Täler bzw. Löcher geprägt sein kann. Zudem verrät die Struktur der umliegenden Funktionswerte, die
von Springstundenminimierung o.ä. geprägt wird, selten die günstigste Richtung zu einem solchen Tal, da es z.B.
ungültige Lösungen mit wenigen Springstunden geben kann.
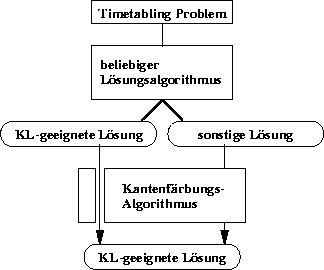
Durch das oben beschriebene Zwischenschalten des Kantenfärbungsalgorithmus werden diese Täler künstlich verbreitert, da
nun die benachbarten Lösungen zu KL-geeigneten Lösungen umgeformt werden.
Es bleiben insbesondere beim RSTP
natürlich auch Täler erhalten, die durch die nichtbeachteten Gruppenmitglieder (s. Abschnitt 6.6.1) erzeugt werden; diese
sind aber nicht so tief. Dies wirkt sich allerdings andererseits
auch so aus, daß nun große Gebiete mit gleichem Funktionswert entstehen, da für viele Punkte bereits die Eingabe
der Zielfunktion identisch ist. Gerade auf der Traversierung solcher Flächen beruhten aber die Fortschritte
moderner Metaheuristiken gegenüber klassischen Minimierungsverfahren.
Zudem muß man sich - im Gegensatz zum Problem der Täler - hiermit nicht abfinden, da man diesen Flächen eine
zusätzliche Struktur aufprägen kann:
- Die weichen Bedingungen können z.T. über der Eingabe des Graphenalgorithmus ausgewertet werden.
- Der Kontrast zwischen einzelnen Werten kann reduziert werden, so daß ein schnellerer Wechsel bei der Ausgabe des Graphenalgorithmus erfolgt.
- Der Abstand zu der Lösung eines relaxierten Problems, z.B. eines LPs, kann hinzugenommen werden, so daß vornehmlich in dessen Nähe gesucht wird.
Innerhalb der Tabusuche gibt es zwei Stellen, die es erlauben, diesen Filterprozess zu integrieren, abgesehen von einer Verwendung als Pre- oder Postprocessor:
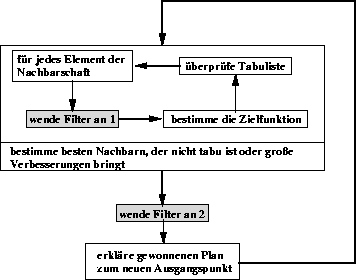
Den oben geäußerten Ideen würde es am besten gerecht, wenn das Filterverfahren in der inneren Schleife (1) integriert würde,
also zu jeder Berechnung der Zielfunktion herangezogen würde. Dies würde aber, um noch eine ausreichende Geschwindigkeit
gewährleisten zu können, verlangen, die Nachbarschaft ausreichend klein zu wählen, so daß die Zahl der Iterationen
entsprechend gedrückt würde.
Eine Möglichkeit dies zu realisieren, wäre eine Form von Metropolis-Verfahren mit Tabuliste,
da hier aus der Nachbarschaft jeweils nur ein Element ausgewählt würde. Hier träte allerdings das Problem auf, daß dieses Verfahren insgesamt
mehr Einzelschritte vollziehen muß als die Tabusuche.
In dieser Arbeit wurde der andere Weg beschritten und das Suchverfahren als nachträglicher Filterschritt vorgesehen, was wesentlich
weniger laufzeitaufwendig ist, aber eher einem memetischen Algorithmus entspricht (vgl. [BNW95]). Dies wiederum
kann dazu führen, daß diese Nachbearbeitung die Veränderungen, die durch das Suchverfahren vorgenommen werden,
revidiert. Um diesem entgegenzuwirken, werden die Zeitstunden vor Anwendung des Filterschritts zufällig permutiert. Die
Wahrscheinlichkeit, ob dies funktioniert, ist allerdings vom jeweiligen Problem abhängig, da es durchaus vorkommen
kann, daß eine bestimmte Schulstunde nur in einer bestimmten Zeitstunde liegen darf.
Um diesem entgegenzuwirken, werden die Zeitstunden vor Anwendung des Filterschritts zufällig permutiert. Die
Wahrscheinlichkeit, ob dies funktioniert, ist allerdings vom jeweiligen Problem abhängig, da es durchaus vorkommen
kann, daß eine bestimmte Schulstunde nur in einer bestimmten Zeitstunde liegen darf.
Geht man allerdings davon aus,
daß keine Zeitwünsche gegeben sind, und daß die entsprechende Stunde nicht mehr von der Wahl der übrigen Stunden beeinflußt wird, so sinkt sie unter 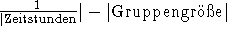 , da der Filter sie
unabhängig von der gewählten Permutation stets im gleichen Bearbeitungsschritt setzt. Die Wahrscheinlichkeit,
daß eine Stellung vollständig rekonstruiert wird, ist entsprechend geringer, aber nicht das Produkt dieser
Wahrscheinlichkeiten, da die Ereignisse nicht unabhängig sind.
, da der Filter sie
unabhängig von der gewählten Permutation stets im gleichen Bearbeitungsschritt setzt. Die Wahrscheinlichkeit,
daß eine Stellung vollständig rekonstruiert wird, ist entsprechend geringer, aber nicht das Produkt dieser
Wahrscheinlichkeiten, da die Ereignisse nicht unabhängig sind.
Nachbearbeitung
Offenbar hat das obige Verfahren den Nachteil, daß bezüglich der nichtbeachteten Gruppenobjekte Widersprüche auftreten können. Ließe man nun einfach die entsprechenden Kanten weg, so würde dies nur dazu führen, daß diese entweder nicht gesetzt werden oder irgendwann zu unbedingt notwendigen Kanten würden, so daß diese dann trotz ihrer Kollisionen eingesetzt werden müßten.
Gestaffelte Ressourcenoptimierung
Wurde nach obigem Verfahren eine Menge von Stunden ermittelt, die in die momentan betrachtete Zeitstunde gelegt werden sollen, so ist noch zu überprüfen, daß diese nicht wegen nicht im Graphen repräsentierter Gruppenmitglieder kollidieren. Im Gegensatz zur Vorgehensweise in Abschnitt 8.4.3 reicht es hier allerdings nicht, nicht setzbare Stunden nur zu markieren, sondern es sollen möglichst viele Stunden gesetzt werden. Dies entspricht aber dem Set-Packing Problem, welches selbst wieder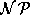 -schwer ist. Standardansatz wäre hier eine LP-Relaxation mit anschließendem Runden (vgl. [Hoc97]), aber der zeitliche Aufwand wäre
für eine Subroutine einer Metaheuristik zu hoch. Glücklicherweise liegt aber ein zusätzliches Kriterium vor, nämlich die
Wichtigkeit der Stunden. Sei also angenommen, es existiere eine vollständige Ordnung O auf den m Stunden, die ausgewählt wurden, und seien diese so
angeordnet, daß
-schwer ist. Standardansatz wäre hier eine LP-Relaxation mit anschließendem Runden (vgl. [Hoc97]), aber der zeitliche Aufwand wäre
für eine Subroutine einer Metaheuristik zu hoch. Glücklicherweise liegt aber ein zusätzliches Kriterium vor, nämlich die
Wichtigkeit der Stunden. Sei also angenommen, es existiere eine vollständige Ordnung O auf den m Stunden, die ausgewählt wurden, und seien diese so
angeordnet, daß 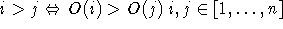 . Dann kann im Abschnitt 8.4.3
analog zu und mit demselben Beweis wie in Abschnitt 6.6.2 eine Bewertung der Kanten vorgenommen werden,
bei der alle Kanten, die in bezug zur Gruppe
. Dann kann im Abschnitt 8.4.3
analog zu und mit demselben Beweis wie in Abschnitt 6.6.2 eine Bewertung der Kanten vorgenommen werden,
bei der alle Kanten, die in bezug zur Gruppe 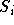 stehen, den Wert
stehen, den Wert 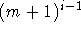 erhalten. Bestimmt man nun ein
maximal gewichtetes Matching in diesem Graphen, so werden zunächst die Gruppen mit hohem Index befriedigt, bevor eine
mit niedrigem Index überhaupt eine einzige Kante erhält. Dieses Verfahren ist natürlich nicht optimal - es wäre es
nur, wenn die Gruppen mit den größten Indices ein maximales Packing bilden würden, aber es ist dennoch dem
Greedy-Verfahren, das Gruppen wählt solange sie passen, überlegen, da dieses auch dann, wenn eines existiert, kein
Matching der bevorzugten Komponenten garantieren kann.
erhalten. Bestimmt man nun ein
maximal gewichtetes Matching in diesem Graphen, so werden zunächst die Gruppen mit hohem Index befriedigt, bevor eine
mit niedrigem Index überhaupt eine einzige Kante erhält. Dieses Verfahren ist natürlich nicht optimal - es wäre es
nur, wenn die Gruppen mit den größten Indices ein maximales Packing bilden würden, aber es ist dennoch dem
Greedy-Verfahren, das Gruppen wählt solange sie passen, überlegen, da dieses auch dann, wenn eines existiert, kein
Matching der bevorzugten Komponenten garantieren kann.Auch wenn nur
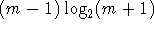 , also polynomiell viele Bits zur Kodierung dieser Gewichtungen benötigt würden,
scheint es im Rahmen dieser konkreten Anwendung sinnvoller, sich mit den zur Verfügung stehenden Zahldarstellungen
zu beschränken, und stattdessen die Gruppen in mehrere Mengen aufzuteilen.
, also polynomiell viele Bits zur Kodierung dieser Gewichtungen benötigt würden,
scheint es im Rahmen dieser konkreten Anwendung sinnvoller, sich mit den zur Verfügung stehenden Zahldarstellungen
zu beschränken, und stattdessen die Gruppen in mehrere Mengen aufzuteilen.Tritt eine Ressource stets im Zusammenhang mit den gleichen dynamischen Ressourcen auf, so könnte wenn man das Matching- durch das analoge Flußproblem ersetzt, diese Ressource den dynamischen vorgeschaltet werden, was die Kollisionszahl vermindern würde, da diese Ressourcen nur noch gleichzeitig oder gar nicht benutzt werden können, wobei die selbe Konstruktion entstehen würde, wie in Abbildung b) in Kapitel 3.6.1. Verzichtet man darauf, die optimale Zuordnung zu wählen, so kann die Existenz auch mit Hilfe des nichtgewichteten Algorithmus geprüft werden (s. Abschnitt 6.7).
Alternierende Kreise
Wird festgestellt, daß eine der gewählten Stunden die vorhandenen Ressourcen überschreitet, so wird versucht, diese zu entfernen. Das hier eigentlich notwendige Konzept wäre das von Matchings mit Ressourcenbeschränkungen, die aber, wie schon in Abschnitt 4.10.7 erwähnt für den gegebenen Fall nicht effizient bestimmt werden können.Wie in Abschnitt 4.3.3.1 dargestellt, ist es bei der Untersuchung verschiedener Matchings in Graphen interessant, deren symmetrische Differenz zu betrachten. Vergleicht man nun zwei maximale Matchings miteinander, so besteht ihre symmetrische Differenz aus Pfaden gerader Länge und Kreisen, da es keine augmentierenden Wege mehr geben darf und somit ein Pfad ungerader Länge immer fortgesetzt werden kann. Wird das Matching über einen alternierenden Kreis modifiziert, bleibt, im Gegensatz zu der Verwendung von Pfaden, die Menge der vom Matching überdeckten Knoten gleich. Insbesondere erhält eine Veränderung nach diesem Schema also die Eigenschaft eines Matchings, Knoten kritischen Grades zu überdecken. Somit bietet sich das Suchen solcher Kreise an, um Matchings nachträglich zu verbessern.
Hierbei muß dafür gesorgt werden, daß die neu hinzugekommenen Kanten nicht andere Ressourcenüberschreitungen verursachen. Daher werden hierfür nur Kanten zugelassen, die nicht mit einer Differenzierungsstunde korrespondieren. Dieses Vorgehen folgt der Überlegung, daß im Bereich des RSTP damit zu rechnen ist, daß sich räumliche Probleme relativ leicht beheben lassen, da es häufig möglich ist, Unterricht auch in Nicht-Fachräumen durchzuführen. Diese Annahme muß bei anderen Planungsaufgaben natürlich nicht gegeben sein.
Betrachtet man den Gesamtwert eines solchen Matchings, so verringert sich dieser bei Alternieren über einen solchen Kreis um das Gewicht der beteiligten Matchingkanten und es vergrößert sich um das der Nicht-Matching-Kanten. Da es
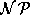 -vollständig ist,
in einem Graphen den längstmöglichen Weg zu suchen, kürzeste Wege auf Netzwerken mit positiven Kantengewichten schneller
bestimmt werden können als auf allgemeinen und es insgesamt wünschenswert ist, den Graphen so wenig wie möglich zu verändern, werden die
Kantengewichte wie folgt modifiziert und als Entfernungen interpretiert, damit der Algorithmus von DIJKSTRA [Jun90] anwendbar wird:
Sei
-vollständig ist,
in einem Graphen den längstmöglichen Weg zu suchen, kürzeste Wege auf Netzwerken mit positiven Kantengewichten schneller
bestimmt werden können als auf allgemeinen und es insgesamt wünschenswert ist, den Graphen so wenig wie möglich zu verändern, werden die
Kantengewichte wie folgt modifiziert und als Entfernungen interpretiert, damit der Algorithmus von DIJKSTRA [Jun90] anwendbar wird:
Sei 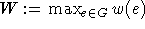 . Dann setze
. Dann setze
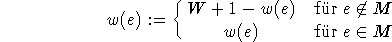
Danach wird solange noch Widersprüche auftreten, aber nur nmal (es muß nicht notwendigerweise möglich sein, alle Kollisionen zu beseitigen) die folgende Routine durchgeführt, wobei die Partitionen des Graphen im folgenden mit links und rechts bezeichnet seien.
- Bestimme eine Kante e=(l,r), die maximal viele Kollisionen auslöst.
- Bestimme den alternierenden Kürzeste-Wege-Baum [Blu98] von r zu allen anderen Knoten auf der rechten Seite (s.u.)
- Bestimme denjenigen Knoten
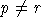 auf der rechten Seite, bei dem die Summe von Entfernung im Baum und Abstand zu l minimal sind.
auf der rechten Seite, bei dem die Summe von Entfernung im Baum und Abstand zu l minimal sind. - Vertausche entlang des durch (l,p), den kürzesten Weg von p zu r und (l,r) gegebenen Kreises Matching - und Nicht-Matching - Kanten.
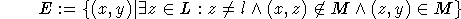
Da dieses z eindeutig bestimmt ist, sei 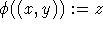 .
.
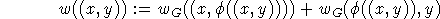
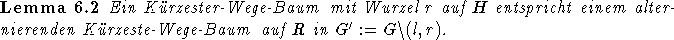
Beweis
Hierzu genügt es, zu zeigen, daß es zu jedem einfachen alternierenden Pfad von R nach R in G einen Pfad gleichen
Gewichtes in H gibt und umgekehrt.
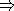 : Jeder von r ausgehende alternierende Pfad muß mit einer Nicht-Matching-Kante
beginnen, da
: Jeder von r ausgehende alternierende Pfad muß mit einer Nicht-Matching-Kante
beginnen, da 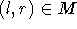 entfernt wurde. Damit erfolgt der Übergang zu einem anderen
entfernt wurde. Damit erfolgt der Übergang zu einem anderen 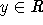 stets über eine Abfolge von
Nicht-Matching-Kante und Matching-Kante und somit muß man, um einen Weg in H zu erhalten, einfach jeden zweiten Knoten
des Weges in G' entfernen. Das Gewicht des Pfades ist nach Definition die selbe.
stets über eine Abfolge von
Nicht-Matching-Kante und Matching-Kante und somit muß man, um einen Weg in H zu erhalten, einfach jeden zweiten Knoten
des Weges in G' entfernen. Das Gewicht des Pfades ist nach Definition die selbe.
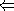 : Sei ein einfacher Pfad in H
: Sei ein einfacher Pfad in H
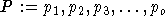 gegeben. Dann wähle den Pfad
gegeben. Dann wähle den Pfad 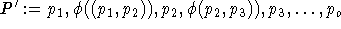 in G.
Dieser hat offenbar die selbe Länge wie P und ist alternierend. Es bleibt nur zu zeigen, daß er einfach ist. Keines der
in G.
Dieser hat offenbar die selbe Länge wie P und ist alternierend. Es bleibt nur zu zeigen, daß er einfach ist. Keines der 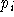 kann doppelt auftreten,
da dann P nicht einfach wäre. Sei also angenommen, daß ein
kann doppelt auftreten,
da dann P nicht einfach wäre. Sei also angenommen, daß ein 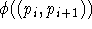 mehrfach
auftritt z.B. als
mehrfach
auftritt z.B. als 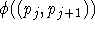 . Da aber die Kante
. Da aber die Kante 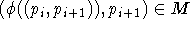 sein muß und
sein muß und 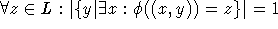 gilt,
da jede Matching-Kante nur zu je einem Knoten in L und R inzident ist, folgt daraus unmittelbar
gilt,
da jede Matching-Kante nur zu je einem Knoten in L und R inzident ist, folgt daraus unmittelbar 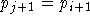 , was wiederum
implizieren würde, daß P nicht einfach war.
, was wiederum
implizieren würde, daß P nicht einfach war.
Das Entfernen von l bzw. (l,r) ist notwendig, da diese benötigt werden, um den Weg zu einem Kreis zu schließen.
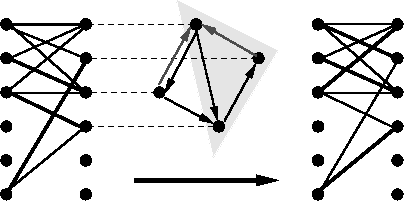
Die Abbildung zeigt einen Alternierungsvorgang, wobei als Kreis in H die grau unterlegten Kanten gewählt wurden.
Gruppen, die nun immer noch nicht mit Ressourcen versehen wurden, werden entfernt bzw. sollte die zugehörige Kante im Graphen kritisch sein, als Kollision in Kauf genommen. Eventuell könnte hier noch versucht werden, weitere Gruppen greedy hinzuzufügen.
Next: Implementierung dieses Verfahrens Up: Verfahren 1: Tabusuche Previous: Wahl der Nachbarschaft (c) Martin Loehnertz 1999