Wahl der Nachbarschaft

Im allgemeinen ([Cos94],[Sch96],[Her92]) werden zwei Stundenpläne als benachbart angenommen, wenn sie durch eine einfache Operation, wie etwa das Verschieben einer Stunde, auseinander hervorgehen. Im folgenden sollen die Auswirkungen einer solchen Verschiebung kurz untersucht werden:
Sei angenommen, daß eine Stunde S aus n Objekten besteht. Es ist natürlich nicht sinnvoll, diese Stunde in eine Zeitstunde zu verschieben, die von einer zur selben Gruppe gehörenden Stunde belegt wird. Ansonsten wird normalerweise jedes Objekt in der neuen Zeitstunde bereits in einer anderen Stunde verwendet. D.h. um diese eine Verschiebung gültig werden zu lassen, müssen bis zu n weitere Gruppen bewegt werden. Im Idealfall sieht das so aus, daß n-1 weitere Gruppen aus der alten Zeitstunde in die neue bewegt werden, so daß in der alten Zeitstunde Platz für die n aus dem neuen Timeslot zu verschiebenden Gruppen gewonnen wird (Kanten deuten Kollisionen an):

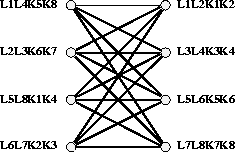
Jede andere Variante würde offenbar noch mehr Stunden involvieren. Für n=2(STP) müssen also insgesamt 4 Stunden bewegt werden. In [Sch96], wo lediglich das STP betrachtet wird, wird dies realisiert, indem als elementare Operation ein Austausch vorgesehen wird, und stets dann, wenn Widersprüche auftreten, ein Korrekturversuch durch eine weitere Austauschoperation unternommen wird, was zum Erfolg führen kann, da somit die benötigte Zahl von Mengenverschiebungen erzielt wird. Für größere n wird dieses Vorgehen aber sinnlos, da der Zeitaufwand für die entstehende 2n-OPT Optimierungsaufgabe zum Lösen der Widersprüche zu aufwendig wird. Gibt man aber diesen harten Bedingungen die größtmögliche Priorität, wird es somit offenbar nahezu unmöglich, ein lokales Minimum der harten Nebenbedingungen zu verlassen. Da somit das Hintereinanderausführen mehrerer Schritte auch kein Verlassen des entsprechenden Gebietes garantieren kann, wird in dieser Arbeit der einfachere Nachbarschafts-Ansatz nach COSTA [Cos94] gewählt, der nur elementare Verschiebeoperationen vorsieht und die Behandlung dieses Problems in den Bereich der Ziel- bzw. Aspiration-Funktion bzw. der Hybridisierung verlagert.

Es sei noch angemerkt, daß diese gerade beschriebene Eigenschaft des Lösungsraums unter den gängigen Metaheuristiken nur mit Tabusuche und Genetischen Algorithmen effektiv angegangen werden kann, da die entsprechenden großen Sprünge der Zielfunktion die Wahrscheinlichkeit, daß z.B. Simulated Annealing\ ein solches Loch verlassen kann, aufgrund des exponentiellen Charakters der Akzeptanzfunktion exponentiell gering werden läßt. ELMOHAMED et al. [ECF97] versuchen daher z.B. die Wahl des neuen Punktes mittels einer Heuristik zu verbessern, was andererseits eine Analyse des erwarteten Verhaltens unmöglich werden läßt.

Aufgrund des obigen Beispiels wurde die Tabuliste asymmetrisch gewählt; d.h. wenn eine Stunde A von einer Stunde B weggelegt wurde, so kann B A folgen, A aber nicht zurückverlegt werden. Ansonsten wäre ein Austausch, wie er oben angedeutet wird, unmöglich. Der relativ große Aufwand zur Berechnung der Zielfunktion läßt es nicht zu, stets die gesamte Nachbarschaft zu betrachten. Es muß daher eine Teilmenge, in diesem Fall eine konkrete Schulstunde ausgewählt werden, deren Verschiebbarkeit getestet werden soll. Dies ließe sich natürlich auch durch eine komplexere Konstruktion der Nachbarschaft erreichen, aber es scheint üblich zu sein, hier diese Terminologie zu verwenden ([Cos94]).

Dieses Vorgehen birgt allerdings ein gewisses Risiko: Als eine der Voraussetzungen für die Funktionsfähigkeit von Tabusuche wird stets angenommen, daß die reflexiv-transitive Hülle der Nachbarschaftsrelation alle Punkte des Lösungsraums paarweise verbindet. Dies ist bei den relativ einfachen Übergangsoperationen stets gesichert. Durch dieses Vorgehen, nun von einer Teilmenge der Nachbarschaft zu sprechen, bleibt der Anschein gewahrt, daß dies nach wie vor gelte. Bei [Cos94] werden hier z.B. nur Stunden betrachtet, die Kollisionen aufweisen. Dies heißt z.B., daß unabhängig von der Wahl der Zielfunktion ein Verlassen einer Konstellation, die die harten Nebenbedingungen erfüllt, nicht möglich ist.
Dieses Vorgehen stellte sich - in ersten Experimenten - als nicht ausreichend heraus, da, wenn die vollständige Beseitigung dieser Probleme nicht möglich ist, nach Ablauf des Programms simple Optimierungschritte möglich bleiben, die aber wegen der zu eingeschränkten Suchweise nicht beachtet wurden. Daher wurde eine gemischte Bewertung nach der Zahl der Widersprüche und der Wartezeit eingeführt. Die Priorität einer Zeitstunde ergibt sich dabei einfach als Summe der Zahl der Ressourcenüberschreitungen und der Wartezeit seit dem Zeitpunkt der letzten Betrachtung dieser Stunde. Da die Zahl der Überschreitungen durch die der Zahl Objekte O beschränkt ist (sei Z die Zahl der Zeitstunden), genügt es also, mindestens O+Z Iterationen durchzuführen, um sicherzustellen, daß jede Zeitstunde mindestens einmal überprüft wurde. Spätestens sobald eine Stunde Wartezeit O erreicht, nimmt die Zahl der Stunden mit höherer Priorität mit jedem Schritt um 1 ab, da jede dieser auf einen Wert kleiner-gleich O zurückgestellt wird. Damit muß die betrachtete Stunde nach spätestens Z weiteren Schritten die höchste Priorität aufweisen. Alle in dieser Zeitstunde gelegenen Schulstunden werden dann der Reihe nach auf Verschiebbarkeit geprüft. Dies stellt zumindest prinzipiell den Zusammenhang des Lösungsraums unter der Teilmenge der Nachbarschaft-Relation sicher, wobei zugleich die verstärkte Untersuchung kollidierender Stunden gesichert wird.

Zusätzlich wird hier jeder Stunde, die eine Kollision aufweist, das Verbleiben in der Zeitstunde verweigert, so daß diese nach Abschluß ihrer Untersuchung sicher kollisionsfrei ist. Dies erscheint zunächst übertrieben, stellt sich aber wiederum im Zusammenhang mit der Zahl der für eine Verbesserung benötigten Operationen als sinnvoll heraus, da somit allein die Möglichkeit geschaffen werden kann, hier mehrere andere Stunden unterzubringen.
Sehr interessant ist hier auch der Ansatz in [Cat98], wo - wenn auch im Kontext des Simulated Annealing - die Möglichkeit vorgesehen wird, Stunden ganz zu entfernen. Hierdurch können die starken Sprünge an den Rändern eines Optimums abgeschwächt werden. Im schulischen Kontext ist die Zahl der möglichen, aber abzulehnenden (Nachmittags-) Stunden ausreichend hoch, um diesen Effekt über eine Verletzung schwächerer Nebenbedingungen zu erzielen. ABRAMSON [AD93] führt dies ebenfalls als möglichen Ausweg an.

Bewertungs und Aspiration - Funktion

Die Bewertungsfunktion ist identisch mit der eingangs beschriebenen. Es werden aber zunächst zwei getrennte Zielfunktionen bestimmt: Sei x eine Konfiguration so ist h(x) die Zahl der Kollisionen und s(x) repräsentiert die verbleibenden Summanden. Anstelle einer Diversifizierung wird nach einer bestimmten Anzahl von Schritten ohne Verbesserung von h dessen Anteil an der Zielfunktion reduziert, was, von den schwachen Nebenbedingungen getrieben, zu einer verstärkten Kompaktifizierung des Planes führt. In dieser Situation wird die Zielfunktion zusätzlich um eine schwache Randomisierung ergänzt, da bei reiner Berücksichtigung der schwachen Nebenbedingungen häufig mehrere Stunden gleich bewertet werden, was zur einer nur von der Stundenreihenfolge geprägten und daher immer identischen Auswahl führen und damit die Zahl der Kollisionen unnötig in die Höhe treiben würde. Da die Größe der Zufallswerte unterhalb der Auflösung der Zielfunktion liegt, könnte die vorliegende Methode im Rahmen der Klassifikation von BATITTI [Bat96] als fixed TS with stochastic tie breaking eingeordnet werden.
Dem Charakter des Lösungsraums entsprechend wurde die Aspiration-Funktion so gewählt, daß sie sowohl auf Verbesserungen der harten, als auch auf eine deutliche Verbesserung im Bereich der weichen Nebenbedingungen anspricht. Konkret bedeutet dies, daß die Aspiration-Funktion dann einem Wechsel zustimmt, wenn die Zahl der Kollisionen um mehr als die halbe Gruppengröße reduziert werden kann, was bei kleineren Gruppen kaum möglich ist, oder wenn ein Ergebnis erzielt werden kann, das besser als das bisher erreichte ist.

Es besteht natürlich nicht die Notwendigkeit, hier die Funktionen einzusetzen, die den tatsächlichen Zielfunktionen des Problems entsprechen; so z.B. erzielen KHANNA et al.[KMSV94] mit abgewandelten Funktionen im Sinne der Ausgangsfunktion bessere Ergebnisse. Ein möglicher Ansatz hier wäre es, die erzielte Dichte in Schulstunden pro Zeitstunde mal Kollisionszahl einfließen zu lassen, da eine kollisionsarme Kompaktheit in einer Stunde das Erreichen der echten Zielfunktion in anderen Stunden begünstigen würde. Der Versuch, die schwachen Constraints stärker zu berücksichtigen, indem zu Beginn die harten Bedingungen völlig ignoriert wurden, führte in jeder Hinsicht zu schlechteren Ergebnissen, was sich mit der Beobachtung von ST¨UBER [StŸ97] deckt, daß die Tabusuche nur erfolgreich ist, wenn die Startposition nicht mehr allzuviele Kollisionen aufweist.