Allgemeine Betrachtungen zum Lösungsraum
Next: Wahl der Heuristik: Die Up: Verfahren 1: Tabusuche Previous: Verfahren 1: Tabusuche
Allgemeine Betrachtungen zum Lösungsraum
Im weitaus größten Teil der Literatur wird das Timetabling Problem analog zu seiner Darstellung als ILP kodiert. In
den jeweiligen Implementierungen werden auch häufig Vektoren ganzer Zahlen verwandt, da somit die Dimension erheblich
reduziert werden kann. Die so kodierten Probleme sind damit aber LP-Methoden vollkommen unzugänglich, da Ungleichheits-Nebenbedingungen auftreten.
Läßt man beim ILP zunächst alle Nebenbedingungen weg, so erhält man einen Hyperwürfel der Dimension |Gruppen 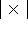 Zeitstunden|.
Bereits die Anforderung, daß genau die gewünschte Zahl von Stunden zu setzen ist, reduziert die Dimension des Lösungsraums derart um
1, daß ein einer Lösung auf dem Hyperwürfel benachbarter Punkt unmöglich gültig sein kann. Dementsprechend
ist bei den meisten Verfahren nicht das Umschalten eines einzelnen Bits, sondern das gleichzeitige Ändern eines
Bits von Null zu Eins und eines anderen von Eins zu Null die Basisoperation. Da zusätzlich die Stunden pro Gruppe
konstant bleiben müssen, reduziert sich dies sogar auf das Verschieben einer Gruppe auf einen anderen Zeitpunkt.
Zeitstunden|.
Bereits die Anforderung, daß genau die gewünschte Zahl von Stunden zu setzen ist, reduziert die Dimension des Lösungsraums derart um
1, daß ein einer Lösung auf dem Hyperwürfel benachbarter Punkt unmöglich gültig sein kann. Dementsprechend
ist bei den meisten Verfahren nicht das Umschalten eines einzelnen Bits, sondern das gleichzeitige Ändern eines
Bits von Null zu Eins und eines anderen von Eins zu Null die Basisoperation. Da zusätzlich die Stunden pro Gruppe
konstant bleiben müssen, reduziert sich dies sogar auf das Verschieben einer Gruppe auf einen anderen Zeitpunkt.
Da die diskrete Zielfunktion nur auf den ganzzahligen und somit am Rande liegenden Punkten definiert ist, stellen
abgesehen von der Ganzzahligkeitsforderung Konvexitätsüberlegungen kein Problem dar, da die konvexe Hülle einer
beliebigen interpolierten Zielfunktion stets an diesen Eckpunkten mit der Funktion selbst übereinstimmt.
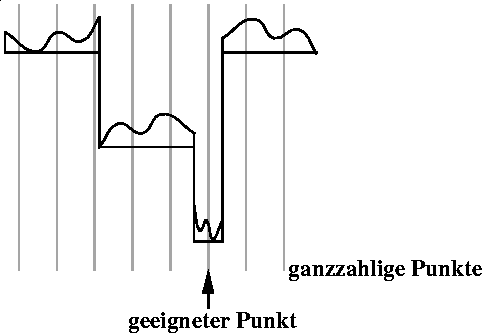
Faltet man den Hyperwürfel auseinander, wobei hier wie bei einem Gray-Code stets nur zwischen benachbarten Punkten gewechselt werden soll, so stellt sich die Oberfläche der Zielfunktion in etwa wie folgt dar:
Auf die von einer Bestrafungs- Funktion zur Erzwingung der harten Bedingungen gebildeten Stufen ist schwächer die Zielfunktion der
weichen Nebenbedingungen aufmoduliert. Da sich harte und weiche Anforderungen zumeist widersprechen, ist eher damit zu
rechnen, daß deren Gradient von den Löchern der Bestrafungsfunktion wegführt, als zu diesen hin.
Wie schon in Unterabschnitt 4.6 erwähnt, tritt bei insgesamt k Zeitstunden jede Lösung der harten Bedingungen
k! mal auf, was aber die Menge der Lösungen im Hyperwürfel nicht dicht werden läßt, da jede nicht gültige Belegung ebenfalls k! mal auftritt.
werden läßt, da jede nicht gültige Belegung ebenfalls k! mal auftritt.
Next: Wahl der Heuristik: Die Up: Verfahren 1: Tabusuche Previous: Verfahren 1: Tabusuche (c) Martin Loehnertz 1999