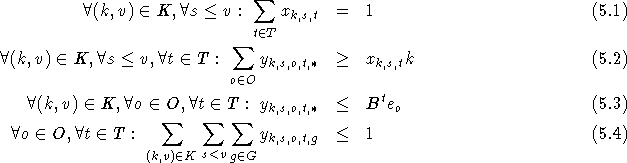Modell
Next: Gesamtaufbau Up: Grundlegende ArchitekturModell und Previous: Problemstellung
Modell
Das betrachtete Problem als ILP
Als Eingabe seien gegeben: Eine Menge von Objekten 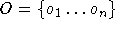 , eine Menge von Mengen
, eine Menge von Mengen 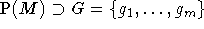 ,
T als Menge von Timeslots und eine Menge von Kursen
,
T als Menge von Timeslots und eine Menge von Kursen 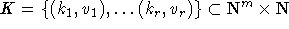 , wobei jeder Koeffizient von k angibt, wieviele
Objekte der entsprechenden Gruppe benötigt werden, und
, wobei jeder Koeffizient von k angibt, wieviele
Objekte der entsprechenden Gruppe benötigt werden, und 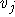 die Vielfachheit des jeweiligen Kurses angibt. Der Einfachheit
halber seien die Gruppenbeziehungen durch eine Matrix
die Vielfachheit des jeweiligen Kurses angibt. Der Einfachheit
halber seien die Gruppenbeziehungen durch eine Matrix 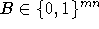 kodiert.
kodiert.
Dann stellt sich das Suchproblem in der folgenden Form dar : Da es der Verständlichkeit dient, werden
die Variablen mit den entsprechenden Objekten anstatt ihrer Indices in den jeweiligen Mengen indiziert:
Finde
: Da es der Verständlichkeit dient, werden
die Variablen mit den entsprechenden Objekten anstatt ihrer Indices in den jeweiligen Mengen indiziert:
Finde
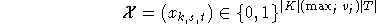
und
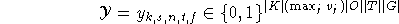
mit
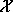 gibt an, zu welchen Zeiten eine Stunde eines Kurses liegt.
gibt an, zu welchen Zeiten eine Stunde eines Kurses liegt. 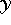 beschreibt, welche Objekte zu welchen Zeitpunkten welchem
Kurs in welcher Funktion zugeordnet werden.
beschreibt, welche Objekte zu welchen Zeitpunkten welchem
Kurs in welcher Funktion zugeordnet werden.
- Bedingung 5.1 gibt an, daß jede Stunde eines Kurses genau einmal stattfindet.
- 5.2 sorgt dafür, daß zu dieser Stunde dem Kurs ausreichend Ressourcen zugeordnet werden.
- Bedingung 5.3 sorgt dafür, daß die Ressourcen nur zu Aufgaben verwandt werden, für die sie geeignet sind. Hier sei
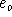 der charakteristische Vektor für o aus
der charakteristische Vektor für o aus
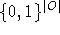 .
. - 5.4 legt fest, daß jedes Objekt pro Zeiteinheit höchstens einmal verwendet werden darf.
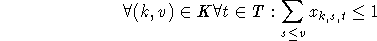
unterbunden werden. Dies wird hier nicht explizit gefordert; einige der Lösungsverfahren produzieren aber nur Lösungen, die dies beachten.
Da es sehr unwahrscheinlich ist, daß dieser Fall vorkommt, wird darauf aber nicht weiter eingegangen.
Daß diese Konstruktion so relativ kompliziert ist, liegt an der Anforderung, die flexiblen Ressourcen nur
zu bestimmten Zeiten auszuwählen. Ließe man hier quadratische Constraints zu, so könnte man bei y die
Zeitdimension sparen. Bei einer durchschnittlichen Schule von 30 Klassen, 40 Lehrern, 40 Räumen, 35
Zeitstunden, im Schnitt 3 Zeitstunden pro Kurs, 10 Kursen pro Klasse und 100 Gruppen ergibt sich eine Zahl von 300 Millionen Variablen. Entfernte man
das Problem flexibler Ressourcen vollständig, wären es nur ca. 31500, d.h. ca. um einen Faktor 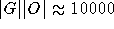 weniger.
Eine ebenfalls mögliche Art der Darstellung ist die, jeweils statt
weniger.
Eine ebenfalls mögliche Art der Darstellung ist die, jeweils statt 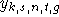 nur
nur 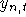 zu verwenden und
als weitere - nur mit ähnlichem Aufwand wie oben darstellbare - Nebenbedingung zu verlangen, daß es eine Abbildung von
zu verwenden und
als weitere - nur mit ähnlichem Aufwand wie oben darstellbare - Nebenbedingung zu verlangen, daß es eine Abbildung von 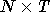 nach
nach 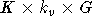 gibt, so daß
die obigen Bedingungen erfüllt sind. Im Zusammenhang mit Abschnitt 8.4.3 erkennt man, daß
bei Festhalten von
gibt, so daß
die obigen Bedingungen erfüllt sind. Im Zusammenhang mit Abschnitt 8.4.3 erkennt man, daß
bei Festhalten von 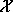 das Bestimmen von
das Bestimmen von 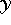 durch ein Matchingverfahren geschehen kann. Daher wird zumeist darauf verzichtet,
durch ein Matchingverfahren geschehen kann. Daher wird zumeist darauf verzichtet,
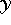 mit zu verwalten, so daß auch hier die Variablenzahl - allerdings auf Kosten der Komplexität - sehr stark verringert werden kann.
mit zu verwalten, so daß auch hier die Variablenzahl - allerdings auf Kosten der Komplexität - sehr stark verringert werden kann.
Zielfunktion
Allen nachfolgend aufgeführten Verfahren wurde eine einheitliche Zielfunktion zu Grunde gelegt. Aus der Menge der
Nebenbedingungen konnten hier natürlich nur die einbezogen werden, für die ein Modellierungsschema vorgesehen ist.
Insbesondere können also Anforderungen, welche Stunden nicht aufeinanderfolgen dürfen o.ä., nicht kodiert werden (siehe hierzu Kapitel 10).
Die Zielfunktion wurde in mehreren Schichten organisiert, so daß sie am besten als lexikographische Ordnung
auf einem Vektor von Zielwerten angesehen werden kann. Dies läßt sich natürlich auch realisieren, indem jeder
Koeffizient des Vektors mit dem Maximalwert des nächsten Koeffizienten gewichtet wird (vgl. Kapitel 6.6.5.1), dies wurde hier aber der
Übersichtlichkeit halber nur in der Kurzanzeige während des laufenden Optimerungsprozesses getan. Die oberste Schicht repräsentiert nochmals die Kollisionsfreiheit, da
diese bei einem der Verfahren nicht als Nebenbedingung auftritt.
Im schulischen Umfeld läßt sich das Konzept Fach nicht umgehen. Daher sei 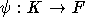 eine Abbildung,
die jedem Kurs das zugehörige Fach zuordnet. Des weiteren sei die Menge der Zeiteinheiten in Tage zerlegt:
eine Abbildung,
die jedem Kurs das zugehörige Fach zuordnet. Des weiteren sei die Menge der Zeiteinheiten in Tage zerlegt: 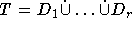 und
dem Zeitverlauf entsprechend angeordnet. Dann baut sich das Ganze wie folgt auf:
und
dem Zeitverlauf entsprechend angeordnet. Dann baut sich das Ganze wie folgt auf:
| Kollisionen | 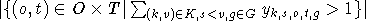 |
| Maximale | |
| Stundenzahl einer | |
| Fach-Klassen-Paarung | 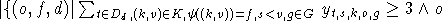 ist Klasse ist Klasse 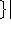 |
| Fach-Klassen-Springstunden | 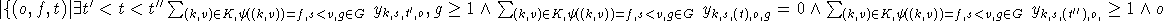 ist Klasse ist Klasse 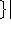 |
| Klassenspringstunden | 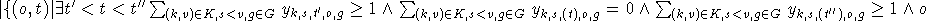 ist Klasse ist Klasse 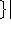 |
| Bevorzugte Zeitpunkte | 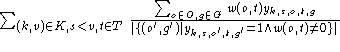 |
| Bevorzugte flexible Objekte | 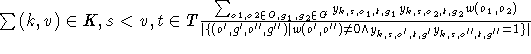 |
| Lehrerspringstunden | 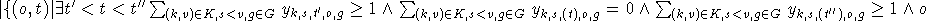 ist Lehrer ist Lehrer 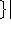 |
Wobei w sowohl das Verhältnis zwischen Objekten, als auch das von Objekten zu Zeiteinheiten angibt. Diese Bewertung kann neutral sein. In diesem Falle wird ein Wert aus den Relationen der betreffenden Übermengen ermittelt (s. Abschnitt 8.4). Der Übersichtlichkeit halber wurde in der Tabelle weggelassen, daß t' und t'' zum selben Tag gehören müssen, wie t.
Der Unterschied
zwischen Klassen- und Lehrerspringstunden muß vom Benutzer angefordert werde (s. Paragraph 8.2.3), da zunächst
kein Unterschied zwischen den Objekttypen vorgesehen ist. Die Normalisierung der Gruppen zueinander erfolgt unter Ausschluß der
Paarungen mit Wert 0, da deren große Zahl Veränderungen in diesem Bereich fast völlig nivellieren würde (vgl. Abschnitt 8.4.2).
Die letzte Subfunktion wird in der Implementierung allerdings nicht exakt so ausgewertet wie hier beschrieben, sondern
es fließen nur diejenigen Paare ein, bei denen das eine ein statisches und das andere ein dynamisches Objekt ist,
Die Beziehung zwischen den festen Objekten ergäbe ohnehin nur eine Konstante, die für alle Lösungen gleich ist;
die Hinzunahme der Beziehungen zwischen flexiblen Objekten ließe selbst die Bestimmung von 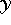 bei feststehendem
bei feststehendem
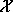
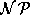 -hart werden (s. Unterkapitel 3.6.1). An einigen Stellen, an denen die Geschwindigkeit der
Auswertung von besonderer Bedeutung ist, wird hier nur festgestellt, wieviele dieser Ressourcen verfügbar sind.
-hart werden (s. Unterkapitel 3.6.1). An einigen Stellen, an denen die Geschwindigkeit der
Auswertung von besonderer Bedeutung ist, wird hier nur festgestellt, wieviele dieser Ressourcen verfügbar sind.
Next: Gesamtaufbau Up: Grundlegende ArchitekturModell und Previous: Problemstellung (c) Martin Loehnertz 1999