Next: Zusammenfassung Up: Lösungsansätze Previous: Weitere Ansätze

Unergiebige Ansätze

Eines der wohl häufigsten Probleme bei dem Versuch, einen Algorithmus für ein Problem zu finden, besteht darin, daß sehr viel Zeit damit verbracht wird, bereits begangene, aber nicht fruchtbare Wege erneut zu untersuchen. Da aber solche Fehlschläge verständlicherweise kaum publiziert werden, läßt sich dies zumeist nicht verhindern. Im folgenden werden einige Versuche aufgeführt, das Timetabling-Problem entweder als lösbare Teilklasse des Problems der Graphenfärbung zu identifizieren oder zumindest Teilaspekte davon zu modellieren, und es wird aufgezeigt, woran diese Versuche jeweils scheitern.

Das Optimum Cost Chromatic Partition Problem

Als schon eher an der Realität der automatischen Stundenplanerstellung entsprechendes Modell bietet sich das OCCP an, bei dem jeder Farbe ein Preis 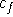zugeordnet wird, und es die Aufgabe ist, den Graphen so zu färben, daß die Summe über die so entstandenen Kosten aller Kanten minimal wird. Dies entspricht insofern einem annehmbaren Ansatz, als es zumeist möglich ist, die Schulstunden vollständig nach ihrer Beliebtheit zu ordnen. Eine Erweiterung stellt das General Optimum Cost Chromatic Partition Problem dar, das dem Timetablingbis auf die relativen Constraints entspricht; hier kann jeder Kanten-Farben-Paarung ein Gewicht zugewiesen werden. Wie JANSEN [Jan97] zeigt, sind beide Probleme für fast alle Arten von Graphen und für sehr eingeschränkte Farbzahlen NP-hart. Effiziente Algorithmen existieren nur für Bäume und für Graphen mit beschränkter Baumweite (treewidth). Auch DeWerra [dW95] zeigt einige auf Bäumen lösbare Timetabling-Probleme mit diversen Nebenbedingungen auf.

Bekannt gutartige Formen von Hypergraphen

Da sich, wie oben dargestellt, University Timetabling und Examination Timetabling auf das Färben von Hypergraphen zurückführen lassen, stellt sich natürlich die Frage, ob bei diesen nicht eine der Teilklassen der Hypergraphen vorliegt, für die Färbungsalgorithmen bzw. Matchingalgorithmen (z.B. [CCKV96]) bekannt sind.

Eine Übersicht über die wichtigsten besonderen Klassen von Hypergraphen findet sich in [Dou95]. Wie aus dem dort gezeigten Diagramm hervorgeht, besitzen fast alle dieser Graphen die sog. Helly-Eigenschaft, nach der Mengen paarweise überschneidender Kanten einen gemeinsamen Knoten besitzen. Dazu sei folgendes Beispiel betrachtet: Gegeben seien zwei Lehrer und zwei Klassen. Es sollen folgende Unterrichtsstunden abgehalten werden: 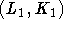, , 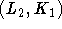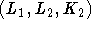. Der zugehörige Hypergraph ist in dem folgenden Diagramm wiedergegeben und besitzt diese Eigenschaft offenbar nicht:

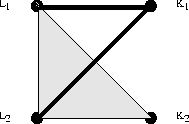
Ebenso lassen sich Beispiele konstruieren, so daß die entsprechenden Graphen nicht perfekt sind.

Andere Ergebnisse zu Kantenfärbungen und Matchings in Hypergraphen

Verwendbare Sätze über die Kantenfärbbarkeit von Hypergraphen gibt es in erster Linie für den Fall, daß eine Färbung zu einer Färbung des korrespondierenden vollständigen Graphen erweitert werden soll (z.B. [Dou95],[HH93],[Bro95]). Diese lassen sich hier nicht anwenden, weil die Farbenzahl dieser vollständigen Graphen wesentlich zu hoch liegt. Zudem bringt die Einführung echter Differenzierungsstunden mit verschiedenen Lehrern und Klassen mit sich, daß die Graphen nicht mehr durch die Trennung nach Objekttypen partitioniert werden können. Die Möglichkeit einer Färbung scheint bei größeren Graphen immer eher gegeben zu sein: Wie PIPPENGER und SPENCER [PS89] zeigen, gibt es für jede Größe einer Differenzierung k und jede Abweichungsanforderung 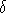ein 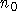und ein 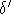, so daß für alle Problemstellungen mit mehr als 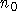Objekten, bei denen die minimale und die maximale Stundenzahl D zweier Objekte keinen größeren Quotienten als 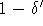aufweisen und der Quotient aus der maximalen Zahl von Stunden, an der zwei identische Objekte beteiligt sind und D ( 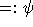) kleiner als 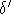bleibt, die maximale Zahl der benötigten Stunden durch 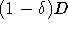beschränkt ist. Hierbei tritt allerdings das Problem auf, daß 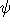im Timetabling-Kontext nicht beliebig klein werden kann, da die maximale Zahl der Stunden in einem Kurs - in der Regel 5 - eine untere Grenze bildet.
Eine Erweiterung des Satzes von HALL auf Differenzierungen, die nur einen Lehrer, aber mehrere Klassen enthalten können, findet sich in [Hax95]. Allerdings läßt sich dies weder auf eine Färbung erweitern, noch zu einem effizienten Algorithmus umgestalten, da das Kriterium selbst wieder auf kleineren Matchings beruht.

PathMatching

Die polynomielle Lösbarkeit einer gemeinsamen Verallgemeinerung der Algorithmen zum maximalen gewichteten Matching und zu Matroidschnitten, die laut VYGEN [Vyg] zu den schwersten noch polynomiell lösbaren Verfahren zählen, ist das von CUNNINGHAM und GEELEN [CG97] untersuchte Path-Matching. Gegeben zwei Matroide (d.h. durch den GreedyAlgorithmus optimal lösbare Probleme), deren Elemente durch unabhängige Knotenmengen repräsentiert werden und ein diese verbindender Graph G, ist es Ziel, knotendisjunkte Pfade zwischen jeweils zwei Elementen zweier Basen (d.h. maximal unabhängiger Mengen) zu finden und die verbleibenden Knoten von G durch ein maximales Matching zu überdecken. Es sieht zunächst so aus, als könne man dieses Problem dazu verwenden, Timetabling-Probleme mit exakten Ressourcenvorgaben (d.h. = statt 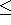) zu lösen, indem man, ausgehend von dem bipartiten Graphen wie er im Satz von K¨ONIG auftritt, die Knoten als die Elemente trivialer Matroide, in denen alle Teilmengen unabhängig sind, interpretiert und jede Kante durch einen Pfad ungerader Länge ersetzt. Verbindet man nun die beiden jeweils mittleren Knoten der Pfade mit einem weiteren Punkt, so würde eine Einbeziehung dieses Knotens in das Matching dafür sorgen, daß nur einer der beiden Pfade existieren kann. Analog könnte man n dieser mittleren Knoten mit m weiteren zu einem vollständigen bipartiten Graphen ( 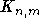) kombinieren, so daß nur n-m dieser Pfade erlaubt wären.

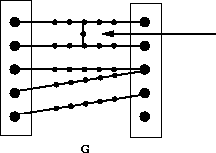
Ungünstigerweise gibt es aber - ähnlich zu den Netzwerkflüssen - keine Möglichkeit, die Pfade daran zu hindern, diese Steuerkanten zu benutzen. Es ist natürlich möglich, eine Kante für einen Pfad undurchquerbar zu gestalten,

aber da beide Endkanten nie zu einem Matching gehören können, könnte man die Kante ohne Implikationen weglassen. Soll also Information durch eine derartige Konstruktion gelangen, so müssen zwei Knoten auftreten, die nicht von allen perfekten Matchings überdeckt werden, sich aber stets gleich verhalten. Dies ist dazu äquivalent, daß es sowohl ein perfektes Matching gibt, das beide überdeckt, als auch eines, das beide nicht überdeckt. Wenn einer nicht überdeckt ist, hat der verbleibende Graph eine ungerade Knotenzahl,was dazu führt, daß ein weiterer Knoten nicht überdeckt ist. Da aber nur 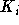und 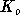Verbindung zum übrigen Graphen haben, ist ein perfektes Matching nur möglich, wenn dies der jeweils andere ist. Ein analoges Argument gilt für den umgekehrten Fall. Aber leider gilt:

Beweis:
Man nehme die symmetrische Differenz S zwischen einem perfekten Matching mit den beiden Knoten ( 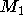) und einem anderen Matching ohne beide Knoten ( 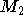). Diese besteht, wie in Abschnitt 4.3.3.1 gezeigt, aus Pfaden und Kreisen. Da jedes der beiden Matchings ganz 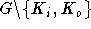überdeckt, hat jeder Knoten darin in der symmetrischen Differenz den Grad 2. Nur 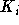und 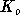haben den Grad 1 und ein Pfad hat somit seinen Endpunkt in ihnen. Da diese beiden aber die einzigen mit Grad 1 sind, muß es sich um denselben Pfad handeln. Weil zu jedem Knoten auf P eine Kante aus 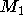inzident ist, die ganz in P liegt, gibt es keine Matchingkanten von P nach 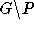. D.h. 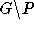besitzt das perfekte Matching .

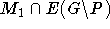Analog läßt sich kein Fall konstruieren, bei dem eine Überdeckung von 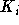äquivalent ist zu einer Nichtüberdeckung von 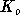, da sich durch das Hinzufügen eines Knotens 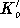und der Kante 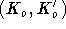dann ein Graph des oben geforderten Typs ergäbe.

Diese Überlegungen schließen natürlich eine generelle Anwendbarkeit des PathMatching nicht aus, insbesondere, da es auch einen gewichteten Fall gibt; es wird lediglich die Unmöglichkeit dieser intuitiven Konstruktion gezeigt. Bei genauerer Betrachtung war ein Funktionieren dieses Vorgehens auch unwahrscheinlich, da es auch das Modellieren des STPs mit Abwesenheitszeiten erlaubt hätte, was - wie gesagt- nach [EIS76] 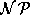-hart ist.

Approximationsalgorithmen für
Multicommodity-Flow Probleme

Wie in Abschnitt 4.3.2 dargestellt, kann das Timetabling-Problem auf Multicommodity-Flüsse reduziert werden, für die ein randomisierter Approximationsalgorithmus mit begrenztem Erwartungswert existiert [Hoc97]. Voraussetzung für dessen Anwendung ist aber, daß die Kantenkapazitäten logarithmisch in der Zahl der Kanten wachsen, was bei der Modellierung der automatischen Stundenplanerstellung leider nicht der Fall ist.

Approximationsschemata für dichte Graphen

Ist die Kantenzahl im Konfliktgraphen bzw. die Zahl der Bedingungen in der entsprechenden logischen (KNF) Formel sehr groß, und gilt es, die Zahl der Konflikte zu minimieren, wie dies z.B. beim Kurswahlproblem der Fall ist, so kann das polynomielle Approximationsschema nach ARORA, KARGER und KARPINSKI [AKK98] angewandt werden: Davon ausgehend, daß sich die optimale Zahl erfüllbarer Nebenbedingungen wie 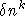verhält, erreicht dieses Verfahren dadurch, daß es zu jedem eine konstante Abweichung von 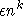garantieren kann, eine multiplikative Abweichung von 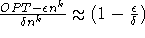, wobei 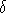meist kleiner gleich 1 ist.
Das Verfahren, dessen genaue Darstellung auch wegen seiner Vielschrittigkeit den Rahmen dieser Arbeit sprengen würde, basiert darauf, ganzzahlige polynomielle Programme (IPP) - in Anlehnung an ILPs - mit einer additiven Abweichung zu lösen, die exponentiell im Grad k des Polynoms ist.

Hierzu wird zunächst eine Probe des Problems logarithmischer Größe genommen, so daß diese mittels eines Backtrackingverfahrens in exponentieller Zeit ihrer Größe, also in polynomieller Zeit der Gesamtgröße des Problems gelöst werden kann. Mit Hilfe der Werte dieser Probe kann ein lineares Programm bestimmt werden, dessen (nichtganzzahlige) Lösung der des Ausgangsproblems mit hoher Wahrscheinlichkeit sehr nahe kommt. Nimmt man nun immer einen Teil der Parameter des Polynoms als konstant an, so daß der verbleibende Ausdruck linear in den übrigen Parametern ist, so können diese gemäß den Rundungsschemata für lineare Programme gerundet werden [Hoc97]. Dabei ist die mögliche Abweichung bei jedem Schritt und mit hoher Wahrscheinlichkeit linear in der Größe des Problems, was dazu führt, daß sie sich jedesmal potenziert und somit am Ende eine Abweichung der Größenordnung von höchstens 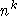zu erwarten ist.
Man kann dieses Verfahren allerdings nicht unmittelbar auf das Problem der Kurswahl anwenden, da jeweils eine Methode gefunden werden muß, um eine Lösung zu finden, die die zunächst nur approximativ erfüllten Nebenbedingungen exakt erfüllt ohne Einbußen bei der Qualität hinnehmen zu müssen. Das am ehesten anwendbare Problem wäre also hier dichtes Max2SAT, wobei sich zusätzlich noch das Problem ergäbe, daß eine Lösung ohne Stunden natürlich ebenfalls alle Nebenbedingungen erfüllen würde. Zudem bleibt in der Praxis auch beim Kurswahlproblem der Maximalgrad durch eine Konstante beschränkt, da andernfalls die Kurse jeweils aufgeteilt würden. Ein Festhalten von bei konstant gehaltenem Maximalgrad würde aber die maximale Größe des Graphen beschränken, was aus denselben Gründen abzulehnen wäre wie ein vollständiges Durchsuchen, das mit Unterstützung durch ILP-Verfahren auf den nächsten Computergenerationen vermutlich möglich wäre. Allerdings stellt, selbst wenn der Grad hoch genug wäre, die Laufzeit ein Problem dar, da es sich nicht um ein voll polynomielles Approximationsschema handelt und die Laufzeit mit 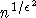wächst, was bereits für relativ große nicht mehr praktikabel ist.
Eine Möglichkeit, diese Algorithmen dennoch anzuwenden, bestünde darin, zuerst solange nach Heuristiken Blockungen zu bilden, bis die benötigte Dichte erreicht ist; hier könnte aber nur experimentelle Laufzeitanalyse endgültigen Aufschluß bieten.

Die ebenfalls in [AKK98] erwähnten Algorithmen für Min-k-CUT ließen sich zwar unmittelbar auf das UTP anwenden, da ein minimaler k-Schnitt auf dem komplementären Graphen einer Färbung entspräche, bei der möglichst wenige Kanten monochromatisch sind, aber die Voraussetzungen sind noch höher, nämlich linear wachender Grad jedes Knotens und o(n) Farben, so daß ein Einsatz im Timetabling-Bereich nicht sinnvoll erscheint.

Sonstiges

Nichtbipartites Matching:
Durch den Übergang zu nichtbipartitem Matching können paarweise Gleichzeitigkeitsbedingungen modelliert werden, indem man zwei Knoten durch einen Pfad ungerader Länge verbindet, und, nach Einfügen einer ausreichenden Zahl von Hilfsknoten, jeweils versucht, perfekte Matchings zu bestimmen (a). Hierbei ergäben die inneren Kanten (Kasten) dann die Stunden, während ein Objekt, daß über eine äußere Kante überdeckt wäre, zum jeweiligen Zeitpunkt frei hätte.
Dieses Verfahren läßt sich aber nicht auf größere Mengen von Knoten ausdehnen, da die einzelnen Konstrukte einander beeinflussen (b). Des weiteren kann nicht mehr garantiert werden, daß alle Knoten maximalen Grades überdeckt werden, da man zwei dieser Knoten mit zwei weiteren synchronisieren könnte, die nicht gleichzeitig gesetzt werden können.

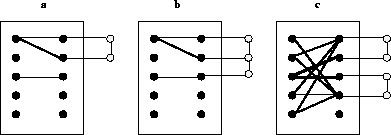
Nichtbipartite Kantenfärbungen:
Gemäß dem Satz von VIZING(1964) kann jeder einfache Graph G mit 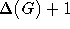Farben kantengefärbt werden [Die96]. Um dies effektiv im Timetablingeinsetzen zu können, müßte dies aber auf Multigraphen übertragbar sein. Wie man aber an einem 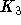mit je n Kanten zwischen den Knoten sieht, bei dem 3n Farben benötigt werden, aber nur ein Maximalgrad von 2n gegeben ist, kann hier die Differenz zwischen 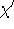und 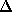beliebig groß werden. Das Edge-Coloring-Problem ist als 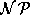-vollständig bewiesen worden, dennoch wird im allgemeinen angenommen, daß es einen Algorithmus gibt, der nur 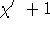Farben benötigt [CR98]; dieser wurde bisher jedoch noch nicht gefunden. Analog zum gerade beschriebenen Matchingansatz könnten dann die Termine zweier Objekte x,y mit höchstens einer Ausname synchronisiert werden, indem man sie mit 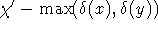zusätzlichen Kanten verbindet, was im bipartiten Fall nur für Objekte verschiedenen Typs möglich ist.

Master-Slave Matchings:
Wie von DEWERRA et al. [dWE96] gezeigt wurde, führt die Nebenbedingung, daß einige (wenige!) Stunden parallel liegen müssen dazu, daß das School-Timetabling-Problem 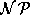-hart wird. Ein schwächere Forderung wäre es zu verlangen, daß bestimmte Lehrer oder Klassen parallel tätig sein sollen. Untersuchungen dazu wurden von [Hef97] vorgenommen, es konnten aber nur Fälle als vielleicht in 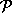identifiziert werden, bei denen der Graph, der Implikationen der Form wenn A Unterricht hat, dann auch B modelliert, aus isolierten Kanten besteht.

Matchings mit Partitionsbeschränkungen:
Eine Möglichkeit, zumindest die Raumbedingungen in das STP zu integrieren, wäre es, bei der jeweiligen Bildung von Paarungen vorschreiben zu können, daß von bestimmten Mengen von Kanten nur jeweils eine bestimmte Anzahl verwendet werden darf. Dieses Problem ist im allgemeinen ebenfalls 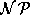-vollständig und nicht konstant approximierbar, wohl aber für eine bestimmte Klasse von Graphen, die sogenannten Pfaffschen Graphen in 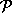. Es wurde hier nicht eingehend untersucht, ob die in der automatischen Stundenplanerstellung auftretenden Graphen tatsächlich nicht pfaffsch sind, aber sämtliche der in [Lec87] angegebenen einfach nachprüfbaren, aber nur hinreichenden Kriterien treffen nicht zu. Selbst wenn die Graphen pfaffsch sein sollten, so hängen beim TimetablingZahl und Größe der Partitionen zumeist linear von der Gesamtproblemgröße ab, was bei den Verfahren in [Lec87], die eine konstante Zahl von Partitionen verlangen, ebenfalls exponentielle Laufzeit hervorruft.
Lediglich bei Beschränkung auf ein STP mit wenigen Raumtypen könnte dieses Verfahren anwendbar sein.

Gradientenverfahren:
Der Übergang zu differenzierbaren Funktionen z.B. auf dem Einheitswürfel dürfte kaum Vorteile bringen, da bei sinnvoller Fortsetzung der auf den Ecken gegebenen Zielfunktion, die hohe Symmetrie des Problems die Gradienten in der Nähe des Mittelpunktes nahezu Null werden ließe. Es verblieben dort also nur die Auswirkungen der schwachen Nebenbedingungen, die ihr Minimum normalerweise nicht in der Nähe eines Minimums der harten Bedingungen haben.

Next: Zusammenfassung Up: Lösungsansätze Previous: Weitere Ansätze