Lokale Suchverfahren: Simulated Annealing undThreshold Accepting
Next: Negotiation Up: Lösungsansätze Previous: Genetische Algorithmen / Evolutionsstrategien
Lokale Suchverfahren: Simulated Annealing und
Threshold Accepting
Das Wesen beider Methoden besteht darin, von einem gegebenen Punkt im Lösungsraum
jeweils zu einem in irgendeinem Sinne benachbarten überzugehen und diese
Veränderung unter bestimmten Bedingungen zu akzeptieren.
Es ist klar, daß die Geschwindigkeit und Leistungsfähigkeit wesentlich von dieser
Nachbarschaftsmenge abhängt: Ist 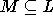 die Menge der akzeptablen Lösungen
im Lösungsraum L, so würde ein Algorithmus für den die Nachbarschaft jedes
Punktes aus M besteht, nach einem Schritt erfolgreich anhalten, während ein anderer,
bei dem sämtliche Nachbarschaften in
die Menge der akzeptablen Lösungen
im Lösungsraum L, so würde ein Algorithmus für den die Nachbarschaft jedes
Punktes aus M besteht, nach einem Schritt erfolgreich anhalten, während ein anderer,
bei dem sämtliche Nachbarschaften in 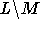 liegen, nie anhält.
liegen, nie anhält.
Da sich ersteres nicht erreichen läßt, ohne M zu kennen, achtet man zumeist darauf, letzteres zu vermeiden, indem man sicherstellt, daß jeder Punkt von jedem anderen in einer endlichen Zahl von Schritten erreicht werden kann. Diese Bedingung ist auch stets Voraussetzung bei Untersuchungen zur Qualität dieser Verfahren [Aar89].
Zur Zeit haben sich die folgenden Varianten etabliert:
- Simulated Annealing:
- In Annäherung an den physikalischen Vorgang des Annealings, des
Abkühlens eines Kristalls, wird jeder bessere Zustand stets und jeder schlechtere
mit einer Wahrscheinlichkeit von
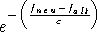 akzeptiert
akzeptiert , wobei c eine rückläufige Temperatur angibt. Auch wenn für das Simulated Annealing inzwischen
auf Markovketten beruhende Analysen zum Laufzeitverhalten vorliegen [Aar89], so sind diese
noch mit Vorsicht zu genießen, da sich Begriffe wie polynomieller Algorithmus ohne
Garantie für die Abweichung o.ä. finden lassen. Ebenfalls von Bedeutung ist die Geschwindigkeit, mit der
der Temperatur-Parameter fällt. ELMOHAMED [ECF97] z.B. schlägt gelegentliches
Wiederaufwärmen vor, wobei in weiterer Analogie zu Abkühlungsprozessen und ihrer Analyse durch die statistische Physik die sogenannte
Phase Transition-Temperatur wieder erreicht werden soll, die den empirisch beobachtbaren Übergangsbereich zwischen der Möglichkeit zu großräumigen
Veränderungen und der lokaler Optimierung darstellt [HHW96].
, wobei c eine rückläufige Temperatur angibt. Auch wenn für das Simulated Annealing inzwischen
auf Markovketten beruhende Analysen zum Laufzeitverhalten vorliegen [Aar89], so sind diese
noch mit Vorsicht zu genießen, da sich Begriffe wie polynomieller Algorithmus ohne
Garantie für die Abweichung o.ä. finden lassen. Ebenfalls von Bedeutung ist die Geschwindigkeit, mit der
der Temperatur-Parameter fällt. ELMOHAMED [ECF97] z.B. schlägt gelegentliches
Wiederaufwärmen vor, wobei in weiterer Analogie zu Abkühlungsprozessen und ihrer Analyse durch die statistische Physik die sogenannte
Phase Transition-Temperatur wieder erreicht werden soll, die den empirisch beobachtbaren Übergangsbereich zwischen der Möglichkeit zu großräumigen
Veränderungen und der lokaler Optimierung darstellt [HHW96]. CATONI [Cat98] gibt durch Einbeziehung einer nicht bestimmten
Invarianten ein Verfahren an, durch das sich die Performanz verschiedener Übergangsmatrizen vergleichen läßt,
ohne auf ein sicheres Konvergenzverhalten zurückgreifen zu müssen. Genauere Untersuchungen zum
Konvergenzverhalten dieses Verfahrens finden sich nur für den Shop-Scheduling-Bereich, der naturgemäß eine
höhere Regularität aufweist als die automatische Stundenplanerstellung [SAW98]. CATONI bietet hierbei unter den betrachteten Arbeiten
das solideste theoretische Fundament, ist aber
auch darauf angewiesen, die Parameter, die in seine Theorie einfließen, experimentell zu bestimmen, wobei er sich auf das Lösen einfacher
Puzzle geringer Größe beschränkt, so daß eine unmittelbare Anwendbarkeit im Timetabling-Bereich auch hier nicht gegeben ist und kein direkter Vorteil
gegenüber dem vollständig versuchsgesteuerten Ermitteln der Parameter zu erkennen ist.
CATONI [Cat98] gibt durch Einbeziehung einer nicht bestimmten
Invarianten ein Verfahren an, durch das sich die Performanz verschiedener Übergangsmatrizen vergleichen läßt,
ohne auf ein sicheres Konvergenzverhalten zurückgreifen zu müssen. Genauere Untersuchungen zum
Konvergenzverhalten dieses Verfahrens finden sich nur für den Shop-Scheduling-Bereich, der naturgemäß eine
höhere Regularität aufweist als die automatische Stundenplanerstellung [SAW98]. CATONI bietet hierbei unter den betrachteten Arbeiten
das solideste theoretische Fundament, ist aber
auch darauf angewiesen, die Parameter, die in seine Theorie einfließen, experimentell zu bestimmen, wobei er sich auf das Lösen einfacher
Puzzle geringer Größe beschränkt, so daß eine unmittelbare Anwendbarkeit im Timetabling-Bereich auch hier nicht gegeben ist und kein direkter Vorteil
gegenüber dem vollständig versuchsgesteuerten Ermitteln der Parameter zu erkennen ist.
- Metropolis-Prozesse
- sind eigentlich die Vorgänger des heute weiter verbreiteten Simulated Annealing und verwenden eine fest gewählte Temperatur. Diese Übergangsmethoden sind zumeist leichter zu analysieren, da die auftretenden Markovketten homogen bleiben.
- Threshold Accepting:
- Hier wird ein schlechterer Punkt akzeptiert, wenn die absolute
Abweichung einen fest vorgegebenen Wert nicht überschreitet. Dieses Verfahren
hat sich laut DUECK [DS90] für einige Probleme dem Simulated Annealing selbst
in deterministischer Ausführung als überlegen erwiesen.
In der Praxis wird die Menge der zu untersuchenden Punkte zumeist dadurch eingeschränkt,
daß bei der Wahl des nächsten Punktes verschiedene Invarianten eingehalten werden, wie z.B. keine Überlappungen für Lehrer. In den meisten Fällen ist die Nachbarschaft durch
diese Eigenschaft bereits vollständig charakterisiert und die Geschwindigkeit der
Konvergenz wird dementsprechend nur über Testläufe ermittelt.
Dennoch liegt der Schwerpunkt im wesentlichen
in der Zielfunktion, die laut [Sch96] bis zu 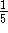 des Programmcodes
ausmachen kann. In Kapitel 6 wird der Versuch unternommen, einen ähnlichen
Effekt durch Hybridisierung mit einem Graphenalgorithmus zu erzielen.
des Programmcodes
ausmachen kann. In Kapitel 6 wird der Versuch unternommen, einen ähnlichen
Effekt durch Hybridisierung mit einem Graphenalgorithmus zu erzielen.
Die sog. Tabusuche wird auch zu den lokalen Suchverfahren gezählt. Eine genauere Beschreibung findet sich in
Abschnitt 6.3, da dieses Verfahren auch im Rahmen dieser Arbeit angewandt wurde.
Next: Negotiation Up: Lösungsansätze Previous: Genetische Algorithmen / Evolutionsstrategien (c) Martin Loehnertz 1999