Constraintbasierte Verfahren
Next: Genetische Algorithmen / Evolutionsstrategien Up: Lösungsansätze Previous: Lineare Programmierung / Ganzzahlige
Constraintbasierte Verfahren
Prinzip
Diese Methode besteht darin, eine Menge von Variablen anzunehmen, für diese
Domains (Wertbereiche) und Constraints\(Relationen) zu definieren und dann
mit Hilfe von Propagationsverfahren, z.B. durch Intervallarithmetik[SM97]  die Domains mehr und mehr einzuschränken,
bzw. neue Constraints zu erzeugen. Im Falle der automatischen Stundenplanerstellung ist die Ausgangsdarstellung zumeist
mit der für ILPs identisch. Zum Lösen der Aufgaben werden entweder fertige Pakete
zur Constraintpropagierung [WZ97] oder Variationen des Verfahrens von GOTTLIEB
([Got63]) eingesetzt. Da dies nach dem Algorithmus nach K¨ONIG, der nicht speziell im
Hinblick auf das Timetabling entstand, der erste echte Algorithmus der automatischen Stundenplanerstellung war, soll er hier kurz
beschrieben werden:
die Domains mehr und mehr einzuschränken,
bzw. neue Constraints zu erzeugen. Im Falle der automatischen Stundenplanerstellung ist die Ausgangsdarstellung zumeist
mit der für ILPs identisch. Zum Lösen der Aufgaben werden entweder fertige Pakete
zur Constraintpropagierung [WZ97] oder Variationen des Verfahrens von GOTTLIEB
([Got63]) eingesetzt. Da dies nach dem Algorithmus nach K¨ONIG, der nicht speziell im
Hinblick auf das Timetabling entstand, der erste echte Algorithmus der automatischen Stundenplanerstellung war, soll er hier kurz
beschrieben werden:
Das Verfahren von Gotlieb
Grundlegend ist es die gleiche Konstruktion, wie sie auch in Abschnitt 4.3.3 verwendet wird. Zusätzlich
werden zwei 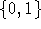 -Vektoren eingeführt, die angeben, zu welchen Zeiten die Lehrer bzw. Klassen verfügbar sind.
-Vektoren eingeführt, die angeben, zu welchen Zeiten die Lehrer bzw. Klassen verfügbar sind. Seien mit
Seien mit 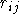 die Anforderungsmatrix, mit
die Anforderungsmatrix, mit 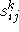 die Verteilung in der kten Stunde und mit t bzw c die oben genannten Vektoren bezeichnet.
die Verteilung in der kten Stunde und mit t bzw c die oben genannten Vektoren bezeichnet.
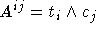 sei als Schreibweise für die Zeiten vereinbart zu denen sowohl Lehrer i, als auch Klasse j zur Verfügung stehen.
Die Mengen der Klassen bzw. Lehrer seien
sei als Schreibweise für die Zeiten vereinbart zu denen sowohl Lehrer i, als auch Klasse j zur Verfügung stehen.
Die Mengen der Klassen bzw. Lehrer seien 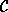 bzw.
bzw. 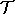 . Die Zeitstunden seien mit
. Die Zeitstunden seien mit 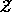 bezeichnet.
Man erhält damit folgende Constraints (bei [Got63] noch Restraints genannt):
bezeichnet.
Man erhält damit folgende Constraints (bei [Got63] noch Restraints genannt):
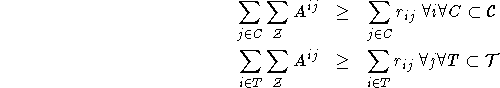
In moderner Sprechweise: Die Hall-Bedingungen für ein Matching zwischen den geforderten Stunden und
den Zeitpunkten zu denen jeweils eine solche Stunde stattfinden kann, müssen erfüllt sein.
Fälle, in denen in einer der obigen Ungleichungen Gleichheit gilt, bezeichnet GOTLIEB als tight und nur in
diesen ist nach seiner Methode eine Restraint-Propagierung möglich: Da bei einer tight Kombination
alle Stunden dafür verwendet werden müssen, können diese für andere Lehrer (Klassen) gesperrt werden. Hiermit
sinken bei verschiedenen anderen Gleichungen die linken Seiten, was zum Beweis der Unlösbarkeit
oder zu neuen tight Kombinationen führen kann. Ist keins davon der Fall, werden solange Stunden
beliebig festgelegt, bis wieder eine solche Menge auftritt. Als zusätzliche Bedingung wird noch angeführt, daß
entsprechend auch ein Matching von den tight Zeitpunkten zurück zu den Lehrern bzw. Klassen möglich sein
muß. GOTLIEB[Got63] gibt allerdings weder eine Reihenfolge der Variablen noch Überlegungen dazu an, wie zeitaufwendig das
Verfahren ist. LIONS [Lio66] reduziert den von ihm auch nicht näher untersuchten Aufwand für
das Überprüfen der Bedingungen durch Einführung des Ungarischen Algorithmus (vgl. Kapitel 6), wobei hier aber
einfaches bipartites Matching als dessen Sonderfall schneller wäre.
Anwendbarkeit
Da die meisten Standardpakete den Raum der verbleibenden möglichen Lösungen nahezu vollständig durchsuchen und zur Eingrenzung nur aus den Constraints, nicht aber aus dem Kontext gewonnene Heuristiken verwenden, dürften sich diese Verfahren durch eine stärkere Abkehr von den fertigen Paketen hin zu Timetabling-spezifischen Lösungen verbessern.
Insbesondere ist es wahrscheinlich nicht hinreichend, sich bei der Untersuchung auf eine
Klassifikation der Constrainttypen zu beschränken, da, wie [KS96] zeigt, bei der reinen Vorgabe von Typen
und ohne Einschränkung ihrer Anwendung die Constraint-Satisfaction-Probleme (CSP) entweder trivial - was das Timetablingnicht ist - oder
MAX-SNP-hart sind.
Modifikationen werden zumeist hinsichtlich der Reihenfolge der Auswertung der verschiedenen
Implikationen und hinsichtlich der Auswahl der fest zu setzenden Variablen vorgenommen. Letzteres ist notwendig, da
zu Beginn nahezu keine Folgerungen möglich sind und deren Anzahl erst mit zunehmender Festlegung immer weiter wächst. Es ist aber wohl so, daß die Bestimmung einer optimalen
Reihenfolge, ebenso wie beim Greedy-Algorithmus (vgl. oben) selbst NP-hart ist. MARTE [Mar98] berichtet sogar, daß diese Verfahren
keine Lösungen mehr liefern, wenn die Zahl der Nebenbedingungen gesenkt wird.
In derselben Arbeit finden sich einige statistisch orientierte Heuristiken zur Wahl der Reihenfolge.
Da diese Methode keine Mechanismen für Optimierungsvorgänge vorsieht, wird sie häufig in Kombination mit anderen Techniken z.B. als Reparaturmechanismus verwendet. Abgesehen von den oben angedeuteten Propagationsversuchen finden sich unter dem Begriff Constraintbasiert aber auch andere Verfahren, bei denen dieses aber nur als Bestandteil der Terminologie verwendet wird, da gemäß einer im KI-Bereich verbreiteten Klassifizierung die automatische Stundenplanerstellung unter die Constraint Satisfaction-Probleme fällt.
Next: Genetische Algorithmen / Evolutionsstrategien Up: Lösungsansätze Previous: Lineare Programmierung / Ganzzahlige (c) Martin Loehnertz 1999