Lineare Programmierung / Ganzzahlige Lineare Programmierung / Semidefinite Programme
Next: Constraintbasierte Verfahren Up: Lösungsansätze Previous: Graphentheoriebasierte Verfahren
Lineare Programmierung / Ganzzahlige Lineare Programmierung / Semidefinite Programme
Lineare Programmierung und Ganzzahlige Lineare Programmierung
Obwohl Lineare Programmierung und Ganzzahlige Lineare Programmierung zum üblichen Methodenrepertoire der kombinatorischen Optimierung gehören, konnten
sie sich erst in den letzten Jahren im Timetabling-Bereich etablieren [Bau97]. Die Größe der
Problemstellung machte ein Herangehen mit Branch & Bound-Verfahren unmöglich und ist auf
in Schulen verfügbarer Hardware auch heute noch nicht praktikabel. Positive Ergebnisse bezüglich der
Gutartigkeit der jeweiligen Polytope, wie sie z.B. beim Vehicle Routing [RF88] gegeben sind, liegen noch nicht vor.
Dafür kann man - entsprechende Flexibilität bei der jeweiligen Institution voraussetzend - nichtganzzahlige Lösungen
dennoch anwenden, indem man entsprechend dem kleinsten gemeinsamen Vielfachen der Nenner der Ergebnisse viele Wochen wählt
und dann ganze Stunden entsprechend den jeweiligen Bruchteilen verteilt.
Dieses Verfahren wird aber in der Regel nur bis zu einer Größe des Hauptnenners von 2 eingesetzt.
Lineare Programme dienen daher primär als Lieferant unterer Schranken für Branch & Bound Verfahren.
Zudem sind lineare Zielfunktionen für das Timetablingzumeist nicht ausreichend. So ist es z.B.
unbefriedigend, wenn 10 Lehrer keine ungünstigen Stunden haben,
einer aber deren 10. Diesem kann abgeholfen werden, indem man annimmt, daß es für jedes
(lineare) Kriterium 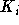 eine von einem Parameter abhängige Funktion
eine von einem Parameter abhängige Funktion 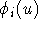 gibt, so
daß für alle u (z.B.
gibt, so
daß für alle u (z.B. 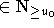 ) gilt, daß jede Lösung mit
) gilt, daß jede Lösung mit 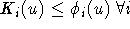 befriedigender ist, als jede, bei der eine der Ungleichungen gebrochen wird. Das
kleinste u, das noch eine solche Lösung zuläßt, könnte mit binärer Suche dann relativ
schnell gefunden werden. Im Timetablingließe sich eine solche Funktion zumeist sehr leicht
angeben, da z.B. eine gleiche Nachmittagsbelastung der Klassen o.ä. zu den
normalen Anforderungen zählt.
befriedigender ist, als jede, bei der eine der Ungleichungen gebrochen wird. Das
kleinste u, das noch eine solche Lösung zuläßt, könnte mit binärer Suche dann relativ
schnell gefunden werden. Im Timetablingließe sich eine solche Funktion zumeist sehr leicht
angeben, da z.B. eine gleiche Nachmittagsbelastung der Klassen o.ä. zu den
normalen Anforderungen zählt.
Wollte man aber versuchen, diese Methode zur weiteren
Optimierung einzusetzen, so stünde man vor dem Problem, eine Teilmenge
der 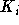 auswählen zu müssen, für die der Wert von
auswählen zu müssen, für die der Wert von 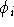 ab sofort anders gewählt werden soll.
Diese Wahl dürfte aber wieder einen exponentiellen Suchaufwand verlangen.
Schränkt man die Suche auf ganzzahlige Probleme ein, so
müßte dann allerdings der entsprechende ILP-Algorithmus für jeden Wert von u erneut gestartet werden.
ab sofort anders gewählt werden soll.
Diese Wahl dürfte aber wieder einen exponentiellen Suchaufwand verlangen.
Schränkt man die Suche auf ganzzahlige Probleme ein, so
müßte dann allerdings der entsprechende ILP-Algorithmus für jeden Wert von u erneut gestartet werden.
Eine Darstellung der Probleme als ILPs wurde bei ihrer Einführung bereits gegeben. Lineare Programme mit mehreren zehntausend Variablen - bei einer mittleren Schule ca. 30000 - können beim heutigen Stand der Technik selbst auf Microcomputern schnell gelöst werden. Relative gewichtete Nebenbedingungen können allerdings nicht modelliert werden. Bei ILPs liegt die Grenze im allgemeinen noch etwas niedriger [MK98], d.h. im Bereich einiger tausend Variablen und es gibt bereits Untersuchungen zu Problemen geringer Größe, bei denen sich ILP z.B. Simulated Annealing überlegen zeigte [BGH97].

Offenbar bilden Pläne, in denen der Lehrer jeweils nur eine Stunde hat, eine Basis des 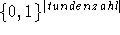 , über dem
diese Funktion modelliert werden müßte. Bei je einer Stunde liegt aber keine Springstunde vor. Des weiteren liegt keine
Springstunde vor, wenn der Lehrer gar keinen Unterricht hat. Somit wäre eine
entsprechende affin-lineare Funktion auf den Vektoren einer Basis und auf dem Nullpunkt Null und somit identisch gleich Null.
, über dem
diese Funktion modelliert werden müßte. Bei je einer Stunde liegt aber keine Springstunde vor. Des weiteren liegt keine
Springstunde vor, wenn der Lehrer gar keinen Unterricht hat. Somit wäre eine
entsprechende affin-lineare Funktion auf den Vektoren einer Basis und auf dem Nullpunkt Null und somit identisch gleich Null.
Dennoch könnte man die Springstundenminimerung in der Form 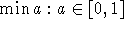
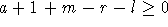 hinzufügen, wobei
die entsprechenden Stunden in der Reihenfolge rml im Plan auftreten. a kann somit nur dann Null sein, wenn
m keine Springstunde ist.
hinzufügen, wobei
die entsprechenden Stunden in der Reihenfolge rml im Plan auftreten. a kann somit nur dann Null sein, wenn
m keine Springstunde ist.
Semidefinite Programme
Einfache quadratische konvexe Probleme lassen sich mit Hilfe
semidefiniter Programmierung darstellen. Diese wiederum kann durch pfadverfolgende Methoden [VB96] oder der Karmakar-Methode für lineare
Programme ähnelnde Verfahren [Ali95] in polynomieller Zeit ausgewertet werden. Sie wird insbesondere in
Approximationsalgorithmen für Graphenfärbungsprobleme [Hoc97] und der Relaxierung von ILP-Problemen eingesetzt.
Ein semidefinites Programm ist gegeben durch eine Menge von Variablen 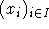 , eine lineare
Zielfunktion
, eine lineare
Zielfunktion 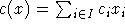 und durch eine Menge symmetrischer
und durch eine Menge symmetrischer Matrizen
Matrizen 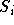 . Das Optimierungsproblem
hat die Form
. Das Optimierungsproblem
hat die Form
Dies kann z.B. dazu verwendet werden, eine gleichmäßige Belastung der Lehrer zu gewährleisten: Wäre z.B.
durch 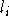 ein Maß für die Belastung eines Lehrers gegeben, so könnte der Ausdruck
ein Maß für die Belastung eines Lehrers gegeben, so könnte der Ausdruck
minimiert werden.
Hierzu muß zunächst das LP, das die gültige Menge beschreibt, in ein Teil des SDP überführt werden. Jedes LP aus Kapitel 2
kann hier eingesetzt werden:
Formt man zunächst die Nebenbedingungen zu 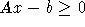 für alle i
um und hat A k Zeilen, so kann man durch Wahl der oberen
für alle i
um und hat A k Zeilen, so kann man durch Wahl der oberen 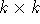 Einträge als
Einträge als
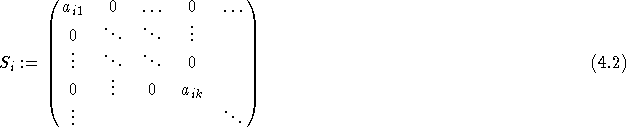
und

wählen, was die entsprechenden Bedingungen garantiert.
Um die obige Optimierungsaufgabe einzubinden, seien zunächst die Hilfsvariablen 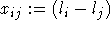 und t hinzugefügt.
Diese Eigenschaft der
und t hinzugefügt.
Diese Eigenschaft der 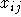 ist linear und kann daher analog zum obigen Vorgehen sichergestellt werden.
Nun fügt man weitere Matrizen
ist linear und kann daher analog zum obigen Vorgehen sichergestellt werden.
Nun fügt man weitere Matrizen 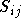 und
und 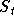 zu der Menge hinzu, so daß sich als deren Summe eine auf der Diagonalen liegende Teilmatrix der Form
zu der Menge hinzu, so daß sich als deren Summe eine auf der Diagonalen liegende Teilmatrix der Form

ergibt. Wie man [VB96] entnehmen kann, sorgt dies dafür, daß 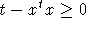 gilt.
gilt. Strebt man nun die Minimierung von t an, so wird offensichtlich auch 4.1 minimiert.
Strebt man nun die Minimierung von t an, so wird offensichtlich auch 4.1 minimiert.
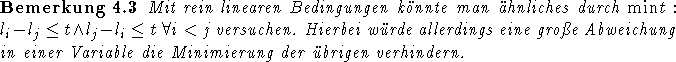

Da die Ränder der Lösungsmenge nicht mehr von konvexen (|I|-1)-dimensionalen Polyedern gebildet werden, wie dies bei den LPs zumeist der Fall ist, muß die Lösung nicht mehr zwangsläufig in einer Ecke liegen, und somit können hier selbst bei ganzzahligen Ecken nichtganzzahlige Lösungen auftreten.
Next: Constraintbasierte Verfahren Up: Lösungsansätze Previous: Graphentheoriebasierte Verfahren (c) Martin Loehnertz 1999