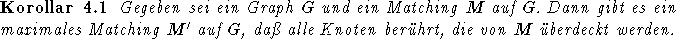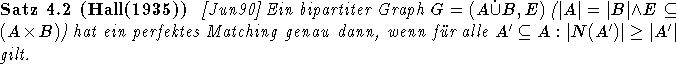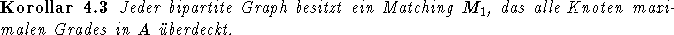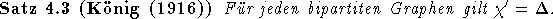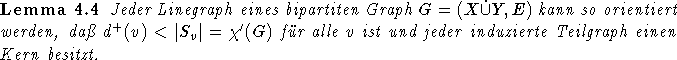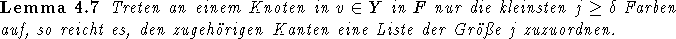Graphentheoriebasierte Verfahren
Next: Lineare Programmierung / Ganzzahlige Up: Lösungsansätze Previous: Wissensbasierte Verfahren / Expertensysteme
Graphentheoriebasierte Verfahren
Wie auch die Heuristiken bewahren diese Verfahren die Invariante, daß kein Objekt zur selben Zeit an zwei verschiedenen Orten sein kann und versuchen, die Zahl der gesetzten Stunden zu erhöhen.
Modellierungsansätze
Aus der Theorie der  -Vollständigkeit ergibt sich, daß jedes
-Vollständigkeit ergibt sich, daß jedes 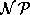 -schwere Problem dazu verwendet werden
kann, das Timetablingzu modellieren. Daher werden im folgenden ausschließlich Beispiele angegeben, die in tatsächlichen
Lösungsversuchen angewandt wurden bzw. bei denen die Modellierung besonders einfach ist.
-schwere Problem dazu verwendet werden
kann, das Timetablingzu modellieren. Daher werden im folgenden ausschließlich Beispiele angegeben, die in tatsächlichen
Lösungsversuchen angewandt wurden bzw. bei denen die Modellierung besonders einfach ist.
Knotenfärbungen:
Jeder Termin, der angesetzt wurde, wird als Knoten eines Graphen repräsentiert.
Zwei Knoten werden genau dann durch eine (ungerichtete) Kante verbunden, wenn die beiden zugehörigen
Termine kollidieren. Offenbar sind dann die Mengen von Terminen, die gleichzeitig stattfinden können, genau die
unabhängigen Knotenmengen. Eine Knotenfärbung dieses Graphen ergibt somit eine gültige Lösung,
wenn man jeder Farbklasse einem Zeitpunkt zuordnet.
Kantenfärbungen:
Hier werden die einzelnen Ressourcen als Knoten und die Termine als (Hyper-)Kanten modelliert.
Zwei Termine kollidieren genau dann, wenn sie einen gemeinsamen Knoten haben. Eine Färbung der Kanten induziert somit wieder
einen gültigen Stundenplan. Diese Darstellung und die des Knotenfärbens
sind durch Cliquen bzw. Linegraphbildung ineinander überführbar.
Netzwerkflüsse:
Das Problem, einen Fluß in einem Netzwerk zu
finden, liegt, wenn keine weiteren Anforderungen gestellt werden, in
zu
finden, liegt, wenn keine weiteren Anforderungen gestellt werden, in 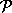 . Daher läßt es sich nur für Spezialfälle wie den folgenden
anwenden: CHAHAL und DEWERRA [CdW89] beschreiben ein Timetabling-Problem, bei dem es egal ist, welcher konkrete Lehrer in
einer Klasse ein Fach gibt, solange nur die Belastungszahlen von Klassen und Lehrern relativ zu den jeweiligen
Fächern eingehalten wird. Hier kann die Bestimmung eines maximalen Matchings, wie sie in Satz 4.3.3 verwendet wird,
als Flußproblem interpretiert und mit einer weiteren Menge von Knoten versehen werden, so daß der Graph dann tripartit wird:
. Daher läßt es sich nur für Spezialfälle wie den folgenden
anwenden: CHAHAL und DEWERRA [CdW89] beschreiben ein Timetabling-Problem, bei dem es egal ist, welcher konkrete Lehrer in
einer Klasse ein Fach gibt, solange nur die Belastungszahlen von Klassen und Lehrern relativ zu den jeweiligen
Fächern eingehalten wird. Hier kann die Bestimmung eines maximalen Matchings, wie sie in Satz 4.3.3 verwendet wird,
als Flußproblem interpretiert und mit einer weiteren Menge von Knoten versehen werden, so daß der Graph dann tripartit wird:
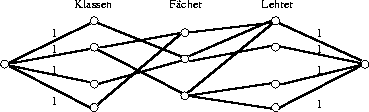
Hierbei repräsentiert die innere Knotenreihe die Fächer und jeder Fluß kann als eine Menge von parallel zu haltenden Stunden interpretiert werden. Die Möglichkeit einer guten Lösung - ohne zusätzliche Bedingungen - ergibt sich aus Kapitel 4.3.3. Zusatzbedingungen - wie z.B. Raumzahlen - lassen sich einbinden, indem man die Fachknoten aufspaltet und zwischen den beiden Duplikaten eine mit der Raumzahl kapazitätsbeschränkte Kante einfügt; hierbei geht die Garantie der Existenz einer Lösung natürlich verloren.
Die ersten beiden Ansätze haben den Nachteil, daß sie keine Modellierung dynamischer Ressourcen erlauben. Eine Konstruktion für einen
Spezialfall im Bereich der Knotenfärbung ergibt sich z.B. [JT95] folgend: Will man bei einer k- Färbung erreichen, daß aus einer gegebenen
Menge M von weniger als k Knoten ein Knoten eine andere Farbe erhält als alle anderen, kann man einen 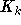 hinzufügen und jeden Knoten aus M mit mindestens
einem Knoten davon verbinden, so daß jeder Knoten des
hinzufügen und jeden Knoten aus M mit mindestens
einem Knoten davon verbinden, so daß jeder Knoten des 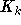 davon überdeckt wird. Offenbar ist eine monochromatische Färbung
von M somit nicht mehr möglich.
davon überdeckt wird. Offenbar ist eine monochromatische Färbung
von M somit nicht mehr möglich.
Es bleibt aber zu zeigen, daß stets eine Färbung gefunden werden kann. Hierzu seien (nach geeigneter Umnumerierung)
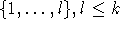 , die Farben von M.
, die Farben von M. 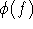 bezeichne ihre Vielfachheit. Ist k=l, so genügt es , eine beliebige fixpunktfreie Permutation
der Farben für die Knoten aus
bezeichne ihre Vielfachheit. Ist k=l, so genügt es , eine beliebige fixpunktfreie Permutation
der Farben für die Knoten aus 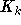 zu wählen. Ansonsten seien die Knoten des
zu wählen. Ansonsten seien die Knoten des 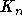 der Farbgröße der zugehörigen Knoten aus M nach sortiert als
der Farbgröße der zugehörigen Knoten aus M nach sortiert als 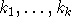 Nun gibt man
Nun gibt man 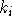 für i<k jeweils die Farbe i+1. Da
für i<k jeweils die Farbe i+1. Da 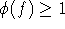 ist, ergibt sich somit leicht per Induktion, daß die Knoten 1 bis k-1 korrekt gefärbt werden.
Da es nach Voraussetzung mehr als eine Farbe gibt, kann der zu Knoten
ist, ergibt sich somit leicht per Induktion, daß die Knoten 1 bis k-1 korrekt gefärbt werden.
Da es nach Voraussetzung mehr als eine Farbe gibt, kann der zu Knoten 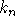 adjazente Knoten aus M nicht die Farbe 1 haben, so daß
adjazente Knoten aus M nicht die Farbe 1 haben, so daß 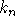 diese erhalten kann.
diese erhalten kann.
Integer Multicommodity Flüsse
Zur Bearbeitung des Gesamtproblems fehlt in klassischen Netzwerkflüssen eine Art Schalter, da
der benötigte Schaltfluß stets auch die dem zu steuernden Fluß zugedachten Kanten verwenden kann.
Die gewünschte Erweiterung des Flußmodells stellen die sogenannten Integer Multicommodity-Flüsse dar. Zugrunde liegt hier
die Vorstellung von mehreren - in diesem Fall zwei - Flüssen, die sich dieselben Netzwerkkapazitäten teilen. Die folgenden zwei Abbildungen beschreiben eine einfache Reduktionsmöglichkeit.
Die folgenden zwei Abbildungen beschreiben eine einfache Reduktionsmöglichkeit.
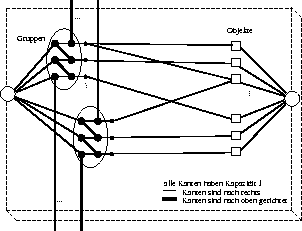
Die Ovale repräsentieren Gruppen von Ressourcenanforderungen, die je eine Unterrichtseinheit bilden: Z.B. Lehrer A + Klasse C + 1 Biologieraum. Die Knoten auf der rechten Seite repräsentieren die verfügbaren Objekte und eine Kante verbindet eine Anforderung mit allen Objekten, die diese erfüllen können. Durch die Anforderungen laufen quer die Kanten eines zweiten Flusses. Der zweite Fluß kann diese Kanten nicht verlassen, da er sonst seine Senke nicht erreichen kann.
Die dargestellten Platten werden wie folgt zusammengesetzt:
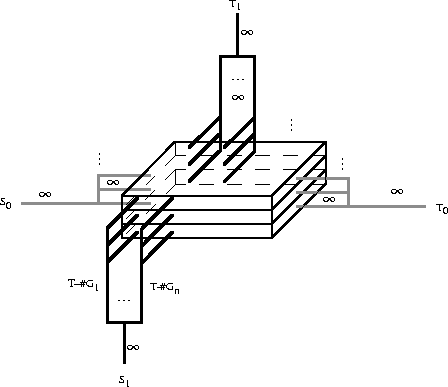
Für jede Zeitstunde wird eine solche Platte eingefügt. Die Kanten des zweiten Flusses werden gruppenweise verbunden und der
Zufluß zu jeder Gruppe erhält als Kapazität die Zahl der Zeitstunden, die diese Gruppe nicht benötigt. Die Summe dieser
Werte über alle Gruppen wird in der Senke angefordert.
Die Verteilerknoten des anderen Flusses werden jeweils mit Quelle und Senke verbunden, wobei an dieser
Senke die Gesamtzahl aller je benötigten Objekte angefordert wird.
Wenn es einen gültigen Stundenplan gibt, gibt es offensichtlich einen Multi-Commodity-Fluß, der das gegebene
Netzwerk befriedigt. Ist umgekehrt ein Fluß gegeben, so müssen alle nicht vom zweiten Fluß blockierten Anforderungen erfüllt werden.
Dies ist aber nur möglich, wenn die entsprechende Anzahl von Stunden der jeweiligen Gruppen mit Ressourcen versehen werden kann.

Hierbei bezeichne T die Zahl der Timeslices und 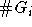 die Zahl der Stunden, die Gruppe i (Lehrer, Klassen, Räume, s. Kapitel 5.3.1) benötigt.
die Zahl der Stunden, die Gruppe i (Lehrer, Klassen, Räume, s. Kapitel 5.3.1) benötigt.
Der Algorithmus nach König
Dieser und der nächste Abschnitt beschreiben auf Kantenfärbungen beruhende Ansätze zur Lösung von Spezialfällen des STP.
Der älteste und wohl bekannteste Algorithmus beruht auf der Tatsache, daß für bipartite Graphen Maximalgrad ( 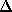 ) und
Kantenfärbbarkeitszahl (
) und
Kantenfärbbarkeitszahl ( 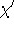 ) übereinstimmen. Diese bereits 1916 von K¨ONIG durch Ergänzung zu
einem regulären Graphen bewiesene Tatsache soll hier nochmals auf anderem
Wege hergeleitet werden:
) übereinstimmen. Diese bereits 1916 von K¨ONIG durch Ergänzung zu
einem regulären Graphen bewiesene Tatsache soll hier nochmals auf anderem
Wege hergeleitet werden:
Einige Grundlagen aus der Matchingtheorie
Als Matching in einem Graphen bezeichnet man eine unabhängige Kantenmenge, d.h. eine Menge von Kanten, die keinen Knoten gemeinsam haben.Wesentliches Element bei der Erzeugung von Matchings sind alternierende Pfade, d.h. Pfade in Graphen, bei denen abwechselnd zum Matching gehörige und nicht zum Matching gehörige Kanten auftreten. Solange ein alternierender Pfad existiert, der mit je einem nicht vom Matching überdeckten Knoten beginnt und endet, kann das Matching weiter vergrößert werden, indem man auf diesem Pfad jeweils Matchingkanten durch Nicht-Matchingkanten ersetzt und umgekehrt. Daß dieses Verfahren hinreichend ist, um maximale Matchings zu erstellen, ist Aussage des Satzes von BERGE.
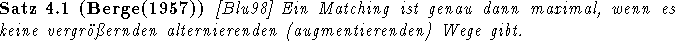
Beweis:
Betrachtet man die symmetrische Differenz zwischen dem gegebenen und einem maximalen Matching,
so hat jeder Knoten einen Grad kleiner-gleich zwei. Damit besteht der Differenzgraph aus alternierenden Wegen und Kreisen.
Da in jedem Kreis genausoviele Kanten des gegebenen, wie des maximalen Matchings auftreten, muß
eine überzählige Kante des maximalen Matchings in einem Weg auftreten, der somit ein augmentierender sein muß.
Dieser Satz besagt insbesondere, daß man mit einem beliebigen Matching beginnen und dieses dann durch Finden alternierender Pfade zu einem maximalen Matching vergrößern kann. Dies liefert das sehr nützliche
Beweis:
Man konstruiere ein maximales Matching M' aus M durch beständiges Alternieren über augmentierende
Pfade. Bei jeder Augmentierung bleiben alle vom ursprünglichen Matching übberdeckten Knoten überdeckt, da an jedem Knoten auch stets
eine Nicht-Matching-Kante innerhalb des Pfades anliegt.
Zum Abschluß dieses Kapitels sei noch einer der wichtigsten Sätze über bipartite Graphen, d.h. Graphen, die sich in zwei innerhalb nicht verbundene Komponenten zerlegen lassen, erwähnt. Im Bereich der automatische Stundenplanerstellung und somit auch im Rest dieser Arbeit werden fast ausschließlich Graphen dieses Typs verwendet.
Der Beweis findet sich in nahezu jedem Buch über Graphentheorie und wird daher und auch wegen seines Umfangs und der Größe des benötigten Begriffsapparates hier nicht wiedergegeben.
Anwendung im Timetabling
Zunächst sollen hier einige unmittelbare Korollare aus Satz 4.2 gezogen werden. Das folgende, eigentlich allgemeinere Ergebnis fällt zumeist als Nebenprodukt des Beweises des Satzes von Hall ab, kann aber auch aus diesem recht einfach bewiesen werden.
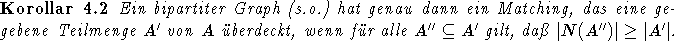
Beweis:
Die Notwendigkeit ist wie im Satz von HALL trivial. Man verbinde nun alle Knoten in 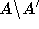 mit allen
Knoten aus B. Der so entstandene Graph G' erfüllt die Voraussetzungen des Satzes von Hall: Enthält eine Teilmenge einen
Knoten aus
mit allen
Knoten aus B. Der so entstandene Graph G' erfüllt die Voraussetzungen des Satzes von Hall: Enthält eine Teilmenge einen
Knoten aus 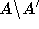 so gilt die Behauptung trivial, ansonsten folgt sie aus der Voraussetzung dieses Korollars. G' besitzt somit ein
Matching, das V(G') und somit auch A' überdeckt. Betrachtet man nun die Kanten, die in A' enden, so bilden sie offenbar
auch in G ein Matching.
so gilt die Behauptung trivial, ansonsten folgt sie aus der Voraussetzung dieses Korollars. G' besitzt somit ein
Matching, das V(G') und somit auch A' überdeckt. Betrachtet man nun die Kanten, die in A' enden, so bilden sie offenbar
auch in G ein Matching.
Mit Hilfe des Schubfachprinzips erhält man:
Mit Hilfe dieser Aussage kommt man schließlich zum folgenden Korollar:
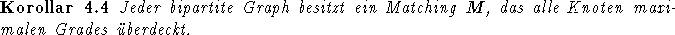
Beweis [Huc]:
Offenbar gibt es mit Korollar 4.3 auch ein Matching, daß alle Knoten maximalen Grades in B überdeckt ( 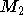 ). Die Frage ist ausgehend von
). Die Frage ist ausgehend von 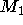 , ob es eines gibt, daß
die verbleibenden Knoten (eventuell ehemals) maximalen Grades in B überdeckt. Hierzu sei zunächst die
Menge der Knoten maximalen Grades in A mit A' bezeichnet (analog B'). Es seien aus
, ob es eines gibt, daß
die verbleibenden Knoten (eventuell ehemals) maximalen Grades in B überdeckt. Hierzu sei zunächst die
Menge der Knoten maximalen Grades in A mit A' bezeichnet (analog B'). Es seien aus 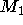 diejenigen Kanten
diejenigen Kanten 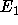 gewählt, die von A' nach B' führen. Diese bilden offenbar ein Matching in dem von
gewählt, die von A' nach B' führen. Diese bilden offenbar ein Matching in dem von 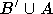 induzierten
Teilgraphen. Gemäß Korollar 4.1 und dem obigen Korollar kann man dieses zu einem Matching
induzierten
Teilgraphen. Gemäß Korollar 4.1 und dem obigen Korollar kann man dieses zu einem Matching 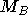 erweitern, daß
ganz B' und
erweitern, daß
ganz B' und 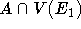 überdeckt. Damit ist
überdeckt. Damit ist 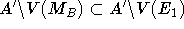 . Für jeden Knoten
. Für jeden Knoten
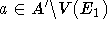 gibt es aber aus
gibt es aber aus 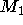 eine Kante nach
eine Kante nach 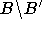 . Nimmt man diese dann zu
. Nimmt man diese dann zu 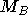 hinzu, wenn
a nicht bereits von
hinzu, wenn
a nicht bereits von 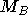 überdeckt wurde, erhält man ein Matching der gewünschten Art.
überdeckt wurde, erhält man ein Matching der gewünschten Art.
Somit erhält man unmittelbar den
Beweis:
Man wähle als Farbklasse stets die Kanten eines Matchings das alle Knoten maximalen Grades überdeckt.
Offenbar sinkt jedesmal der Maximalgrad im Graphen der noch nicht gefärbten Kanten um 1. Damit sind nach
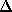 Schritten alle Kanten gefärbt.
Als maximales Ergebnis dieses Sachverhalts für einen Algorithmus zur automatischen Stundenplanerstellung erhält man somit
das folgende Lemma:
Schritten alle Kanten gefärbt.
Als maximales Ergebnis dieses Sachverhalts für einen Algorithmus zur automatischen Stundenplanerstellung erhält man somit
das folgende Lemma:

Die zu diesen Lehrern bzw. Klassen assoziierten Knoten werden im folgenden als kritisch bezeichnet. Dieser Satz ermöglicht es, den Algorithmus von König als Teilroutine anderer Verfahren zu verwenden. Siehe hierzu Kapitel 6.
Der Satz von Galvin
Lange Zeit gab es gegenüber den Verfahren von K¨ONIG keinerlei Verbesserungen [dW85]. Mit dem Beweis der Vizingschen Listenfärbungsvermutung für bipartite Graphen durch Galvin ergibt sich für allgemeine Vorgaben- und Unverfügbarkeitszahlen ein wohl für das School-Timetabling\ endgültiges Ergebnis, sofern man keine spezifischen Forderungen an die Unverfügbarkeiten stellt.

Beweis:
[Die96] Der Beweis verläuft in zwei Schritten. Zunächst wird gezeigt, daß
jeder gerichtete Graph, dessen sämtliche induzierten Teilgraphen einen sog. Kern haben, und
der für alle 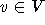
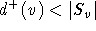 erfüllt, mit den
erfüllt, mit den 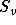 listenfärbbar ist. Dann wird bewiesen,
daß jeder Linegraph eines bipartiten Graphen so orientiert werden kann, daß diese Bedingungen für Listen der
Größe
listenfärbbar ist. Dann wird bewiesen,
daß jeder Linegraph eines bipartiten Graphen so orientiert werden kann, daß diese Bedingungen für Listen der
Größe 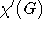 gelten. Da in bipartiten Graphen
gelten. Da in bipartiten Graphen 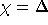 gilt, folgt somit die
gilt, folgt somit die 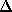 -Kanten-Listenfärbbarkeit
bipartiter Graphen und daraus wegen
-Kanten-Listenfärbbarkeit
bipartiter Graphen und daraus wegen 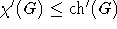 die Aussage des Satzes.
die Aussage des Satzes.
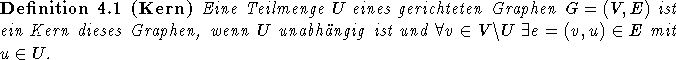
Das Wesen der Methode besteht nun darin, die Bedingung 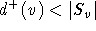 zu erhalten, indem man
jedesmal, wenn
zu erhalten, indem man
jedesmal, wenn 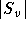 verkleinert wird, sicherstellt, daß auch
verkleinert wird, sicherstellt, daß auch 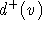 reduziert wird.
reduziert wird.
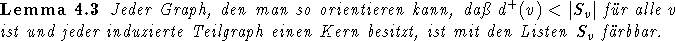
Beweis:
Der Beweis erfolgt durch Induktion. Der leere Graph kann offenbar mit 0 Farben
gefärbt werden. Sei nun H=(V,E) mit obigen Eigenschaften gegeben. Sei eine
Farbe  beliebig gewählt und sei D derjenige Teilgraph von H, der
von den Knoten v mit
beliebig gewählt und sei D derjenige Teilgraph von H, der
von den Knoten v mit 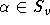 erzeugt wird. Dann besitzt D nach
Voraussetzung einen Kern U. Man färbe nun alle Knoten in U mit
erzeugt wird. Dann besitzt D nach
Voraussetzung einen Kern U. Man färbe nun alle Knoten in U mit  und entferne
und entferne
 aus allen Listen in
aus allen Listen in 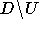 . Da alle Knoten, deren Liste verkleinert wird,
mit U verbunden waren, sinkt deren Ausgangsgrad ebenfalls um eins und
. Da alle Knoten, deren Liste verkleinert wird,
mit U verbunden waren, sinkt deren Ausgangsgrad ebenfalls um eins und 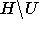 erfüllt die oben gestellten Bedingungen. Nach Induktion ist
erfüllt die oben gestellten Bedingungen. Nach Induktion ist 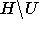 mit den Farbmengen
mit den Farbmengen 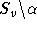 färbbar, und somit gilt die Behauptung.
färbbar, und somit gilt die Behauptung.
Beweis:
Im folgenden wird weiterhin vom Graphen G die Rede sein. Da das eigentliche Objekt der Betrachtungen der zugehörige Linegraph ist, werden nun Kanten zwischen Kanten auftreten.
Es sei eine beliebige (herkömmliche) Färbung von G mit den Farben 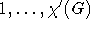 gegeben. Treffen sich zwei Kanten in X, so
sei die Kante zwischen ihnen von der mit der größeren Farbe zu der mit der kleineren Farbe gerichtet. Treffen sie
sich in Y, sei die Orientierung umgekehrt.
gegeben. Treffen sich zwei Kanten in X, so
sei die Kante zwischen ihnen von der mit der größeren Farbe zu der mit der kleineren Farbe gerichtet. Treffen sie
sich in Y, sei die Orientierung umgekehrt.
Zunächst ist zu zeigen, daß 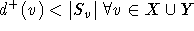 . Sei dazu
. Sei dazu  fest gewählt.
Alle Nachbarn von
fest gewählt.
Alle Nachbarn von  , die Nachfolger von
, die Nachfolger von  bezüglich der Kanten des Linegraphen sind, treffen
bezüglich der Kanten des Linegraphen sind, treffen
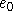 in einem Punkt in X bzw. in einem Punkt von Y. Die Kanten in X haben alle kleinere und paarweise verschiedene Farben als
in einem Punkt in X bzw. in einem Punkt von Y. Die Kanten in X haben alle kleinere und paarweise verschiedene Farben als
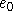 ; die Kanten in Y haben größere und paarweise verschiedene Werte. Damit kann es maximal
; die Kanten in Y haben größere und paarweise verschiedene Werte. Damit kann es maximal 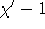 dieser Kanten geben.
Zu
dieser Kanten geben.
Zu 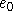 parallele Kanten sind entweder in X oder in Y Nachfolger von
parallele Kanten sind entweder in X oder in Y Nachfolger von 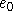 . Damit gefährdet ihre
Existenz die Gültigkeit der Aussage nicht.
. Damit gefährdet ihre
Existenz die Gültigkeit der Aussage nicht.
Als zweites ist zu zeigen, daß jeder Teilgraph einen Kern besitzt. Die Aussage gilt offenbar
für leere Teilgraphen. Somit kann die Aussage wie folgt durch Induktion bewiesen werden:
Es sei gezeigt, daß die Aussage für Graphen mit n Kanten gelte. Sei nun ein beliebiger Teilgraph
D mit n+1 Kanten gewählt. Für 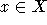 sei
sei 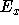 die Menge der mit x inzidenten Kanten und
die Menge der mit x inzidenten Kanten und 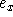 diejenige
Kante aus
diejenige
Kante aus 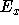 mit minimaler Farbe. Sei
mit minimaler Farbe. Sei 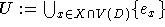 . Offenbar hat jede Kante
in D einen Nachfolger in U, da jede Kante einen Knoten aus X trifft. Dies gilt ebenfalls für
parallele Kanten. Insbesondere wird von zwei parallelen Kanten immer nur eine in U sein. Ist U
also unabhängig, so ist U ein Kern. Es sei also angenommen, daß U nicht unabhängig ist, sich also
zwei Kanten e,e' mit o.B.d.A. c(e')>c(e) in Y treffen. Man entfernt nun e und erhält einen Teilgraph D' mit
n Kanten, der nach Voraussetzung einen Kern U' besitzt. Ist e' in U', so ist wegen der Existenz der
Kante (e,e') U' auch ein Kern von D.
. Offenbar hat jede Kante
in D einen Nachfolger in U, da jede Kante einen Knoten aus X trifft. Dies gilt ebenfalls für
parallele Kanten. Insbesondere wird von zwei parallelen Kanten immer nur eine in U sein. Ist U
also unabhängig, so ist U ein Kern. Es sei also angenommen, daß U nicht unabhängig ist, sich also
zwei Kanten e,e' mit o.B.d.A. c(e')>c(e) in Y treffen. Man entfernt nun e und erhält einen Teilgraph D' mit
n Kanten, der nach Voraussetzung einen Kern U' besitzt. Ist e' in U', so ist wegen der Existenz der
Kante (e,e') U' auch ein Kern von D.
Ansonsten gibt es eine Kante 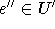 , die von e' aus erreicht wird. Träfen sich e'' und e' in
X, so wäre c(e'')<c(e'), was der ursprünglichen Wahl von e' widerspricht. Somit treffen sie sich
in Y, was c(e'')>c(e') impliziert, woraus wegen c(e')>c(e) c(e'')>c(e) folgt, was wiederum
die Existenz der Kante (e,e'') erzwingt. Somit ist U' ein Kern von D.
, die von e' aus erreicht wird. Träfen sich e'' und e' in
X, so wäre c(e'')<c(e'), was der ursprünglichen Wahl von e' widerspricht. Somit treffen sie sich
in Y, was c(e'')>c(e') impliziert, woraus wegen c(e')>c(e) c(e'')>c(e) folgt, was wiederum
die Existenz der Kante (e,e'') erzwingt. Somit ist U' ein Kern von D.
Wiederum ergibt sich kein Konflikt bei mehrfachen Kanten.
Dies ergibt sich unmittelbar aus den Anmerkungen.
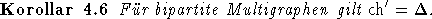
Dies folgt aus dem vorigen Korollar und Satz 4.3.3.

Beweis:
Jeder Kante e sei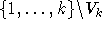 als Farbliste zugewiesen.
Diese Liste ist n.V. größer als
als Farbliste zugewiesen.
Diese Liste ist n.V. größer als 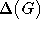 . Somit existiert nach obigem Korollar eine gültige
Listenfärbung.
. Somit existiert nach obigem Korollar eine gültige
Listenfärbung.Damit kann also im klassischen STP jeder Kante eine Menge von verbotenen Timeslots zugeordnet werden, die der Größe nach durch die Differenz der Zahl der möglichen Stunden und der maximalen Stundenzahl einer Klasse (bzw.eines Lehrers) beschränkt ist. Bei normalerweise 39 verfügbaren Schulstunden und 33 Klassen-Wochenstunden entspräche dies also 6 Stunden. [Tuz97] erwähnt, daß sich dieses Ergebnis noch soweit verschärfen läßt, daß jede Liste nur soviele Farben enthalten muß, wie der größere Maximalgrad der inzidenten Knoten. Dies bringt im Timetablingaber keinen Vorteil, da nahezu alle Klassen stets zu fast allen Zeitstunden Unterricht haben, der obige Wert sich also nie sonderlich vom Maximalgrad des Graphen unterscheidet.
Der Beweis des Satzes von Galvin ist so konstruktiv, daß sich ein Algorithmus unmittelbar ableiten läßt (vgl. [Sli96]):
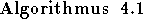
- Färbe den Graphen mit
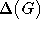 Farben z.B. mit dem Algorithmus aus Abschnitt 4.3.3.
Farben z.B. mit dem Algorithmus aus Abschnitt 4.3.3. - Richte die Kanten des Linegraphen wie im Beweis beschrieben.
- Für jede Farbe
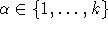 :
:
- Sei D der von den Kanten e mit
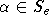 erzeugte Teilgraph des Linegraphen.
erzeugte Teilgraph des Linegraphen. - Setze D'=D.
- Wähle U aus D' wie oben beschrieben.
- Solange U nicht unabhängig ist,
- wähle zwei adjazente Kanten in U und entferne aus D' diejenige mit der kleineren Farbe,
- bestimme U erneut aus D'.
- Färbe die Kanten aus U mit
 , entferne sie aus D und entferne
, entferne sie aus D und entferne  aus allen Farblisten.
aus allen Farblisten.
- Sei D der von den Kanten e mit
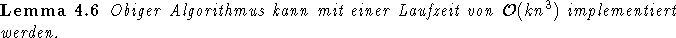
Beweis:
Sei o.B.d.A |X|=|Y|=n und m die Zahl der Kanten. Die Listen seien durch eine Farben-Kanten Matrix repräsentiert.
Der Algorithmus nach K¨ONIG bestimmt k ungewichtete Matchings in jeweils bipartiten Graphen, was
in 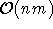 [Blu98]
[Blu98] zu bewerkstelligen ist. Nach jeder Bestimmung eines Matchings können alle Kanten
im Linegraphen, die Kanten des letzten Matchings (die die bisher größte Farbe erhalten) mit Kanten kleinerer
Farbe verbinden (und umgekehrt), sofort erzeugt werden. Da jede Kante maximal mit
zu bewerkstelligen ist. Nach jeder Bestimmung eines Matchings können alle Kanten
im Linegraphen, die Kanten des letzten Matchings (die die bisher größte Farbe erhalten) mit Kanten kleinerer
Farbe verbinden (und umgekehrt), sofort erzeugt werden. Da jede Kante maximal mit 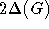 Kanten verbunden ist,
läßt sich der Aufwand dafür mit diesem Wert abschätzen.
Da für das jeweils nächste Matching die jeweils nächstgrößte Farbe gewählt wird, können
die zu einem Knoten gehörigen Kanten und die Farben-Kanten-Matrix gleichzeitig der Farbgröße nach sortiert werden.
Somit erhält man für die Schritte 1 und 2,
die hier gleichzeitig behandelt werden, eine Laufzeit von
Kanten verbunden ist,
läßt sich der Aufwand dafür mit diesem Wert abschätzen.
Da für das jeweils nächste Matching die jeweils nächstgrößte Farbe gewählt wird, können
die zu einem Knoten gehörigen Kanten und die Farben-Kanten-Matrix gleichzeitig der Farbgröße nach sortiert werden.
Somit erhält man für die Schritte 1 und 2,
die hier gleichzeitig behandelt werden, eine Laufzeit von 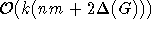 , wobei
, wobei 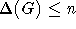 gilt.
gilt.
Die nun folgende Schleife wird k mal ausgeführt.
Der Teilgraph kann über die Matrix in 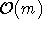 bestimmt werden und aufgrund der Sortierung kann gleichzeitig U daraus erzeugt werden, indem bei jedem vorangegangenen Entfernen nicht zum Teilgraphen gehörender
Knoten aus Y ein Zeiger, der stets auf die Kante mit minimaler Farbe zeigt, auf das nächstgrößere, nicht gelöschte gesetzt wird. Dies setzt voraus, daß die Kanten-Farben-Matrix entsprechend ihrer Sortierung
abgearbeitet wird. Das abschließende Auslesen von U geht in
bestimmt werden und aufgrund der Sortierung kann gleichzeitig U daraus erzeugt werden, indem bei jedem vorangegangenen Entfernen nicht zum Teilgraphen gehörender
Knoten aus Y ein Zeiger, der stets auf die Kante mit minimaler Farbe zeigt, auf das nächstgrößere, nicht gelöschte gesetzt wird. Dies setzt voraus, daß die Kanten-Farben-Matrix entsprechend ihrer Sortierung
abgearbeitet wird. Das abschließende Auslesen von U geht in 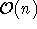 .
.
Der Test auf Unabhängigkeit benötigt 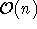 Schritte, da sich die entsprechenden Kanten nur in Y
schneiden können und es somit ausreicht, die bereits überdeckten Knoten in Y zu markieren und ein nicht unabhängiges Paar
daran zu erkennen, daß einer nochmals markiert werden soll. Das Entfernen einer Kante und das
Neuberechnen von U sind wiederum aufgrund der Sortierung in
Schritte, da sich die entsprechenden Kanten nur in Y
schneiden können und es somit ausreicht, die bereits überdeckten Knoten in Y zu markieren und ein nicht unabhängiges Paar
daran zu erkennen, daß einer nochmals markiert werden soll. Das Entfernen einer Kante und das
Neuberechnen von U sind wiederum aufgrund der Sortierung in 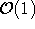 möglich, da beim Entfernen einer
Kante nur jeweils die Kante mit der nächstgrößeren Farbe am selben Knoten aus X diese ersetzt. Es müssen höchstens
m Kanten entfernt werden, um Unabhängigkeit zu erzielen. Damit ergibt sich eine Gesamtlaufzeit von
möglich, da beim Entfernen einer
Kante nur jeweils die Kante mit der nächstgrößeren Farbe am selben Knoten aus X diese ersetzt. Es müssen höchstens
m Kanten entfernt werden, um Unabhängigkeit zu erzielen. Damit ergibt sich eine Gesamtlaufzeit von
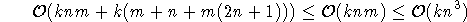
Im Timetabling-Kontext ist zumeist 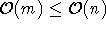 , da Lehrer und Klassen eine beschränkte Stundenzahl haben, und der
Algorithmus hätte hier somit eine Laufzeit von
, da Lehrer und Klassen eine beschränkte Stundenzahl haben, und der
Algorithmus hätte hier somit eine Laufzeit von 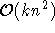 , was der des Algorithmus nach K¨ONIG für diese Fälle
entspricht.
, was der des Algorithmus nach K¨ONIG für diese Fälle
entspricht.
Der Algorithmus läßt drei Freiheitsgrade für weitere Verbesserungen. Zum einen könnte überprüft werden, ob es möglich ist, jeweils andere Kerne zu wählen oder die Reihenfolge der Farbwahl zu variieren, zum anderen ist es möglich, die Ausgangsfärbung analog zu Abschnitt 6.6 zu modifizieren. Hier tritt allerdings das Problem auf, daß obiger Algorithmus bereits gültige Ausgangsfärbungen nicht erhält, wie das folgende Beispiel zeigt. Dabei seien für alle Punkte beide Farben zulässig; die dicken Kanten tragen Farbe 2:

Die oben dargestellte Färbung ist offensichtlich gültig. Der Algorithmus würde nun zunächst alle Kanten in U aufnehmen, dann aber die obere Kante aus U entfernen, da sie die kleinere Farbe an y hat. Damit würden zwei Kanten, die in der gültigen Ausgangsfärbung verschiedene Farben hatten, nun die gleiche Farbe erhalten. Dies ist auch nicht weiter verwunderlich, da die Werte der Ausgangsfärbung durch eine andere Wahl der Reihenfolge im zweiten Schritt des Algorithmus teilweise außer Kraft gesetzt werden können.
Dennoch läßt sich durch Modifikation dieser Färbung etwas erreichen:
Im Bereich der automatische Stundenplanerstellung ist es häufig so, daß nur einige Objekte von Bedingungen betroffen sind. Daher ergibt
sich in geringfügiger Abweichung von der Bestimmung der Listenfärbbarkeitszahl die Frage,
wie klein man irgendeine bestimmte Liste wählen kann. Hier nutzt der Satz von GALVIN die
Kraft seiner beiden Lemmata nicht voll aus, da 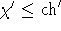 unmittelbar klar ist, und
sich die Frage nach unterschiedlich großen Listen beim reinen Beweis der Viezingschen Vermutung nicht stellte.
Durch striktere Interpretation kommt man somit zu dem:
unmittelbar klar ist, und
sich die Frage nach unterschiedlich großen Listen beim reinen Beweis der Viezingschen Vermutung nicht stellte.
Durch striktere Interpretation kommt man somit zu dem:

Die Frage ist also, unter welchen Umständen man gezielt den Ausgangsgrad eines Knotens
des Linegraphen H reduzieren kann. Dies ist offensichtlich nicht möglich, wenn beide
Knoten, zu denen die entsprechende Kante inzident ist, den Grad 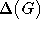 aufweisen.
Nimmt man aber an, daß einer (o.B.d.A der in Y) geringeren Grad hat, so kann man durch geeignete Wahl der
Farbe dieser Kante e in F erreichen, daß der Grad in H entsprechend sinkt, z.B. indem
man e in F die kleinstmögliche Farbe gibt. Damit hat e um eins geringeren Ausgangsgrad in H, als
der zugehörige Knoten in Y Nachbarn, da alle in X e treffenden Kanten somit Vorgänger von e in
H sind. Gibt man dann der nächsten Kante die zweitkleinste Farbe, so ist in X ein Nachfolger möglich,
die Zahl derer in Y reduziert sich aber um 1. Insgesamt erhält man
aufweisen.
Nimmt man aber an, daß einer (o.B.d.A der in Y) geringeren Grad hat, so kann man durch geeignete Wahl der
Farbe dieser Kante e in F erreichen, daß der Grad in H entsprechend sinkt, z.B. indem
man e in F die kleinstmögliche Farbe gibt. Damit hat e um eins geringeren Ausgangsgrad in H, als
der zugehörige Knoten in Y Nachbarn, da alle in X e treffenden Kanten somit Vorgänger von e in
H sind. Gibt man dann der nächsten Kante die zweitkleinste Farbe, so ist in X ein Nachfolger möglich,
die Zahl derer in Y reduziert sich aber um 1. Insgesamt erhält man
Beweis:
Hat die Kante e mit der l. größten Farbe an 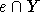 die Farbe p, so
ist
die Farbe p, so
ist 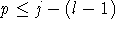 , da die übrigen l-1 Kanten Farben aus dem Intervall (p,j] erhalten
müssen. Andererseits können nur noch diese l-1 der Kanten, die ebenfalls an diesem Knoten
in Y anliegen, Nachfolger von e in Y sein. In X kann es maximal p-1 Nachfolger geben, da
es nur entsprechend viele kleinere Farben gibt. Somit hat e maximal j-(l-1)-1+(l-1)=j-1 Nachfolger. Somit
ist
, da die übrigen l-1 Kanten Farben aus dem Intervall (p,j] erhalten
müssen. Andererseits können nur noch diese l-1 der Kanten, die ebenfalls an diesem Knoten
in Y anliegen, Nachfolger von e in Y sein. In X kann es maximal p-1 Nachfolger geben, da
es nur entsprechend viele kleinere Farben gibt. Somit hat e maximal j-(l-1)-1+(l-1)=j-1 Nachfolger. Somit
ist 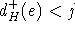
Man könnte nun also versuchen, die Tatsache, daß nur diese j Farben auftreten damit
zu erzwingen, daß man den entsprechenden Kanten in G bei dieser Vorfärbung Listen
der Größe 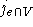 zuordnet, die nur die ersten
zuordnet, die nur die ersten 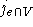 Farben enthalten. Was zunächst
wie ein reiner Zirkelschluß aussieht, liefert dann aber letztlich doch den
Farben enthalten. Was zunächst
wie ein reiner Zirkelschluß aussieht, liefert dann aber letztlich doch den

Beweis:
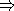 ist trivial, da der Spezialfall auch zu allen Fällen
gehört.
ist trivial, da der Spezialfall auch zu allen Fällen
gehört.
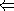 ergibt sich, indem man Lemma 4.7 auf jeden Knoten in Y anwendet.
ergibt sich, indem man Lemma 4.7 auf jeden Knoten in Y anwendet.
Das Ganze gilt symmetrisch auch für die andere Komponente, wobei hier die j größten Farben verwendet werden müßten. Dieser Satz bestätigt somit die intuitiv klare Tatsache, daß der schlechtestmögliche Fall der ist, wenn alle Lehrer (Klassen) gleichzeitig abwesend sind.
Beweis
Offenbar stellt eine Färbung, in der nur die kleinsten 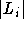 Farben in jeder Liste
Farben in jeder Liste 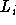 auftreten,
einen geeigneten (polynomiell überprüfbaren) Beweiskandidaten dar.
auftreten,
einen geeigneten (polynomiell überprüfbaren) Beweiskandidaten dar.

equitable colorings
Häufig wird verlangt, daß sowohl Lehrer als auch Klassen an jedem Tag gleichstark
beansprucht werden. Weisen alle Tage gleichviele Stunden auf, so kann dies
mit Hilfe von equitable Colorings\([dW96]) erreicht werden. Eine Kantenfärbung wird als
equitable (balanciert) bezeichnet, wenn für jeden Knoten die Zahl der inzidenten
Kanten jeder Farbe ungefähr gleich ist. Genauer: Ist 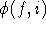 die Häufigkeit des Auftretens
von Farbe f an Knoten i, so gilt für alle Knoten i und für alle Paare von
Farben
die Häufigkeit des Auftretens
von Farbe f an Knoten i, so gilt für alle Knoten i und für alle Paare von
Farben  :
: 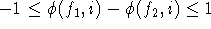 .
.
Eine solche Färbung mit k
Farben kann gefunden werden, indem jeder Knoten v in 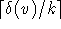 Hilfsknoten
vom Grad k, mit möglicherweise einer Ausnahme, aufgespalten wird und
auf dem so gebildeten Graphen eine normale Kantenfärbung vorgenommen wird. Identifiziert man
danach alle Hilfsknoten wieder mit dem Original, so erhält man eine
Färbung des gewünschten Typs, da mindestens
Hilfsknoten
vom Grad k, mit möglicherweise einer Ausnahme, aufgespalten wird und
auf dem so gebildeten Graphen eine normale Kantenfärbung vorgenommen wird. Identifiziert man
danach alle Hilfsknoten wieder mit dem Original, so erhält man eine
Färbung des gewünschten Typs, da mindestens 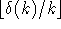 mal und höchstens
mal und höchstens
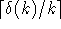 mal die gleiche Farbe an einem Knoten vorliegt.
mal die gleiche Farbe an einem Knoten vorliegt.
Zusätzlich kann erreicht werden, daß die einzelnen Lehrer-Klassen-Kombinationen gleichmäßiger
in der Woche verteilt liegen (vgl. [dWM95]).
Ist 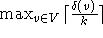 kleiner gleich der Zahl der Zeitstunden
an einem Tag l, so kann das equitable Scheduling zu einem normalen Stundenplan
erweitert werden, indem der Algorithmus nach K¨ONIG auf die jeweils von den Kanten einer Farbe induzierten
Teilgraphen angewandt wird, da deren Maximalgrad dann kleiner als l ist.
kleiner gleich der Zahl der Zeitstunden
an einem Tag l, so kann das equitable Scheduling zu einem normalen Stundenplan
erweitert werden, indem der Algorithmus nach K¨ONIG auf die jeweils von den Kanten einer Farbe induzierten
Teilgraphen angewandt wird, da deren Maximalgrad dann kleiner als l ist.
Next: Lineare Programmierung / Ganzzahlige Up: Lösungsansätze Previous: Wissensbasierte Verfahren / Expertensysteme (c) Martin Loehnertz 1999