Zusammenfassung
Next: Lösungsansätze Up: Komplexität des Problems Previous: Der Normalfall
Zusammenfassung
Ergäbe die obige Reduktion des Knotenfärbens stets sinnvolle Stundenpläne, so wäre der Fall nahezu hoffnungslos.
Bei der beschriebenen Konstruktion tritt aber für jede Kante ein neues Objekt auf, d.h. die Zahl der Objekte wäre bis zu
quadratisch in der Zahl der Schulstunden. In der Realität ist es aber so, daß diese nur ungefähr ein Zehntel der Schulstundenzahl beträgt.
Allerdings ist es bisher nicht gelungen, daraus einen Vorteil zu gewinnen, da die meisten Sätze zu diesen Problemen hier keinen
Unterschied vorsehen, so daß eine Anwendbarkeit stets 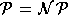 nach sich ziehen würde.
nach sich ziehen würde.
Solange es nicht gelingt, weitere, dem Sachkontext inhärente Nebenbedingungen zu identifizieren, die das Problem
einfacher werden lassen, muß das Problem als nicht lösbar, ja nicht einmal mit konstantem Faktor randomisiert approximierbar angesehen werden.
Dies äußert sich auch in der großen Zahl alchemistisch anmutender Lösungsversuche, bei denen einige nicht theoretisch,
sondern rein experimentell gefundene Parametersätze als Errungenschaften angesehen werden.
Die aufgrund der Verschiedenheit
der Problemstellungen fehlende Vergleichbarkeit dieser Ergebnisse laßt auch einen Versuch der Parameterbestimmung im
größeren Rahmen nicht zu, vgl. unten und [CK95a], die den besten Einblick in die Härte des Problems bieten.
Beiträge über die Approximierbarkeit des Timetabling-Problems sind bisher nicht erschienen. Untersuchungen hierzu wurden jedoch bereits in [Sch95] als lohnendes
Ziel erwähnt.
Die Lösbarkeit einiger Teilprobleme stellt zumindest die prinzipielle Anwendbarkeit informatischer Prinzipien im
Bereich der automatische Stundenplanerstellung sicher.
(c) Martin Loehnertz 1999