Randomisierte Algorithmen/Heuristiken
Next: Die Komplexität von Teilproblemen Up: Komplexität des Problems Previous: Approximierbarkeit
Randomisierte Algorithmen/Heuristiken
Auch die besten randomisierten Algorithmen können weder in der Zahl der Zeitstunden, noch der nicht gesetzten Schulstunden eine Abweichung um einen
konstanten Faktor versprechen (s. [Hoc97]).
Die Ergebnisse, die hier im Bereich des Schedulings erzielt wurden, liefern Grenzen, die im Bereich der
doppelten Zahl der tatsächlich zur Verfügung stehenden Zeitstunden liegen, da sie im übertragenen Sinne zumeist auch
Schulstunden beliebiger Länge verwalten könnten. Zudem zeigen die obigen Ergebnisse, daß eventuell existierende
Algorithmen nicht derandomisiert werden können, da die Nichtexistenz
des somit zu erreichenden
deterministischen Algorithmus dies ausschließt. Da aber für die meisten für dieses Gebiet vorliegenden Verfahren
Derandomisierungsschemata gegeben sind, die die Laufzeit deutlich aber nur polynomiell verschlechtern, würde ihre
Anwendbarkeit sofort 
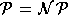implizieren.
Die beweisbare Performanz (nichtderandomisierbarer) randomisierter lokaler Suchverfahren, wie z.B. Simulated Annealing (vgl. Kapitel 4.7), liegt zumeist in der Größe
des Lösungsraums ([Hoc97],[ECF97]), was sie vom theoretischen Standpunkt her einem einfachen Enumerieren aller Varianten
äquivalent werden läßt, wobei die Bedeutung der Tatsache, daß sie tatsächlich eine Lösung finden können [Aar89], nicht herabgesetzt werden soll.
Dennoch ist es so, daß diese Verfahren, auch wenn keine Schranken gezeigt werden können und nur - überwiegend nicht vergleichbare -
numerische Ergebnisse vorliegen, auf den Problemfällen der Realität bessere Lösungen finden, als die oben angesprochenen
Verfahren, da sie sämtliche Nebenbedingungen berücksichtigen können, während das GOCCP als allgemeinstes
theoretisches Modell weder relative Nebenbedingungen noch einen Belastungsausgleich über nichtlineare Zielfunktionen unterstützt.
(c) Martin Loehnertz 1999