Terminologie
Next: Polynomiell lösbare Fälle Up: Komplexität des Problems Previous: Komplexität des Problems
Terminologie
Da überwiegend Reduktionen auf graphentheoretische Probleme vorgenommen werden, bedient sich dieser Abschnitt in verstärktem Maße dem zugehörigen Begriffsapparat. Die hier definierten Ausdrücke werden auch in Kapitel 4 und in Abschnitt 6 verwandt, weshalb die Beschreibung etwas umfangreicher ausfällt, als eigentlich notwendig. Die hier eingeführte Terminologie folgt im wesentlichen der von DIESTEL [Die96], wobei im folgenden kurz auf einige weniger geläufige Begriffe eingegangen wird.
- Linegraph:
- Zu einem Graphen (Hypergraphen) G ist L(G)=(E,K) mit E=E(V) und
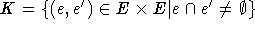 ; d.h.
die Ecken von L(G) repräsentieren die Kanten von G, und zwei Ecken von L(G) sind genau dann verbunden, wenn die entsprechenden
Kanten einen Knoten gemeinsam haben.
; d.h.
die Ecken von L(G) repräsentieren die Kanten von G, und zwei Ecken von L(G) sind genau dann verbunden, wenn die entsprechenden
Kanten einen Knoten gemeinsam haben.
- Cliquengraph:
- Gegeben ein Graph («Hypergraph) G repräsentiert der Cliquengraph CL(G) jede Clique von G durch einen Knoten, und zwei Cliquen sind genau dann miteinander verbunden, wenn sie einen Knoten in G gemeinsam haben.
- Listenfärbung:
- Zu jedem zu färbenden Objekt wird eine Liste von k Farben assoziiert, die für die
Färbung verwendet werden dürfen. Die minimale Listengröße
 , die unabhängig von der Wahl der Farben in den Listen
eine Färbung zuläßt, wird als Listenfärbbarkeitszahl bezeichnet. Diese ist größer-gleich der Färbbarkeitszahl
und im Fall des
, die unabhängig von der Wahl der Farben in den Listen
eine Färbung zuläßt, wird als Listenfärbbarkeitszahl bezeichnet. Diese ist größer-gleich der Färbbarkeitszahl
und im Fall des 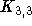 , der 2-färbbar aber nicht 2-listenfärbbar ist, erkennt man, daß Ungleichheit vorliegen kann.
, der 2-färbbar aber nicht 2-listenfärbbar ist, erkennt man, daß Ungleichheit vorliegen kann.
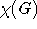 | Knotenfärbbarkeitszahl |
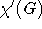 | Kantenfärbbarkeitszahl |
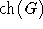 | Knoten-Listenfärbbarkeitszahl |
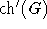 | Kanten-Listenfärbbarkeitszahl |
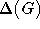 | max. Knotengrad |
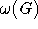 | max. Größe einer Clique |

Die zusätzliche konstante Abweichung bewahrt an dieser Stelle u.a. vor Problemen mit OPT(I)=0.

Next: Polynomiell lösbare Fälle Up: Komplexität des Problems Previous: Komplexität des Problems (c) Martin Loehnertz 1999