Raumverteilung (Room Allocation)
Next: Nachbargebiete Up: Übersicht über das Spektrum Previous: Prüfungsverteilung (Examination-Timetabling)
Raumverteilung (Room Allocation)
Informelle Beschreibung:
Obwohl das Problem der Raumzuteilung ein Teilproblem von STP bzw. UTP ist, konnte es sich als eigenständiges Gebiet etablieren, da
insbesondere im universitären Bereich die Veranstaltungszeiten von jedem Dozenten einzeln und häufig ohne Koordination mit seinen
Kollegen beschlossen werden, und somit der Verwaltung die Aufgabe zufällt, für die notwendigen Räumlichkeiten zu sorgen. Ebenfalls von
Bedeutung ist, daß bereits dieses Teilproblem als in einigen Fälle 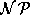 -hart bewiesen wurde [CT92]. Die einfachste
Variante ist in
-hart bewiesen wurde [CT92]. Die einfachste
Variante ist in 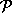 : Gegeben Mengen von Veranstaltungen, die jeweils gleichzeitig stattfinden sollen, finde eine
Zuordnung von Veranstaltungen zu Räumen.
: Gegeben Mengen von Veranstaltungen, die jeweils gleichzeitig stattfinden sollen, finde eine
Zuordnung von Veranstaltungen zu Räumen. 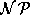 -hart wird
das Problem, sobald man verlangt, daß bestimmte Veranstaltungen stets denselben Raum benutzen sollen (s. Kapitel 3).
-hart wird
das Problem, sobald man verlangt, daß bestimmte Veranstaltungen stets denselben Raum benutzen sollen (s. Kapitel 3).
Darstellung als ILP:
Für den einfachen Fall ergibt sich, da die Zeitstunden getrennt betrachtet werden, eine orthogonale Summe von Matching-Polytopen, die nach von Neumann [Pul95]
ganzzahlige Ecken haben. Es genügt, ein einzelnes zu beschreiben, wobei hier bereits angenommen sein soll, daß durch
Hinzufügen von Hilfsobjekten die Zahl von Stunden und Räumen gleich ist, so daß wahlweise die i oder j die Räume
bzw. Stunden repräsentieren sollen und die 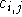 angeben, wie sehr ein bestimmter Raum für eine bestimmte Kursstunde geeignet ist.
angeben, wie sehr ein bestimmter Raum für eine bestimmte Kursstunde geeignet ist.

Nebenbedingungen:
- bestimmte Veranstaltungen sollen stets im selben Raum stattfinden
- Distanzprobleme: Es muß jedem Teilnehmer möglich sein, seinen jeweils nächsten Raum in der Pause zu erreichen (relative Nebenbedingung!)
- eine fortlaufende Veranstaltung sollte die Räume zwischenzeitlich nicht wechseln müssen.
(c) Martin Loehnertz 1999