Realistische Problemstellungen sind #tex2html_wrap_inline5312#-vollständig
Next: Approximierbarkeit Up: Komplexität des Problems Previous: Polynomiell lösbare Fälle
Realistische Problemstellungen sind 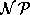 -vollständig
-vollständig
In [EIS76] wurde erstmals ein recht allgemeines Timetabling-Problem als 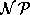 -vollständig nachgewiesen. Dennoch ist dieser
Beweis nicht vollständig zufriedenstellend, da das Konstrukt ein ausgesprochen unrealistisches Stundenplanproblem verwendet.
Zahlreiche Reduktionen
-vollständig nachgewiesen. Dennoch ist dieser
Beweis nicht vollständig zufriedenstellend, da das Konstrukt ein ausgesprochen unrealistisches Stundenplanproblem verwendet.
Zahlreiche Reduktionen 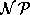 -vollständiger Probleme für verschiedene (einfache) Erweiterungen
des STP finden sich in [CK95a] und [dWMP93], aber auch hier werden überwiegend
unrealistische Fälle verwendet. Da die verwendeten Methoden - auch wegen der Art der Konstrukte - nicht
instruktiv bezüglich eines möglichen Lösungsverfahrens erscheinen, wird an dieser
Stelle auf eine umfassende Darstellung verzichtet. Die
-vollständiger Probleme für verschiedene (einfache) Erweiterungen
des STP finden sich in [CK95a] und [dWMP93], aber auch hier werden überwiegend
unrealistische Fälle verwendet. Da die verwendeten Methoden - auch wegen der Art der Konstrukte - nicht
instruktiv bezüglich eines möglichen Lösungsverfahrens erscheinen, wird an dieser
Stelle auf eine umfassende Darstellung verzichtet. Die 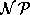 -Vollständigkeit des in dieser Arbeit
untersuchten Problems geht zudem auch aus der im nächsten Kapitel beschriebenen
Reduktion des Graphenfärbungsproblems hervor.
-Vollständigkeit des in dieser Arbeit
untersuchten Problems geht zudem auch aus der im nächsten Kapitel beschriebenen
Reduktion des Graphenfärbungsproblems hervor.
(c) Martin Loehnertz 1999