Polynomiell lösbare Fälle
Next: Realistische Problemstellungen sind -vollständig Up: Komplexität des Problems Previous: Terminologie
Polynomiell lösbare Fälle
Wie in Satz 4.3.3 gezeigt wird, liegt das STP ohne Nebenbedingungen in 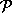 . Gemäß Kapitel 4.3.5
können zudem einige Gleichgewichtsbedingungen berücksichtigt werden. Aus der engen Verbindung zur Graphentheorie
ergeben sich zudem einige Fälle, die gut lösbar sind, da es für sie Darstellungen als LPs gibt, für die die
zugehörigen Polyeder ganzzahlige Ecken haben. Diese sind jedoch mit Ausnahme der ersten drei Fälle so eingeschränkt, daß eine praktische Anwendung nicht abzusehen ist. Daher soll
über diese, die zumeist von DEWERRA ([dW97] [dW96]) gefunden wurden, lediglich eine tabellarische
Übersicht gegeben werden. Auf die ersten drei Fälle wird in Abschnitt 4.10 nochmals näher eingegangen
. Gemäß Kapitel 4.3.5
können zudem einige Gleichgewichtsbedingungen berücksichtigt werden. Aus der engen Verbindung zur Graphentheorie
ergeben sich zudem einige Fälle, die gut lösbar sind, da es für sie Darstellungen als LPs gibt, für die die
zugehörigen Polyeder ganzzahlige Ecken haben. Diese sind jedoch mit Ausnahme der ersten drei Fälle so eingeschränkt, daß eine praktische Anwendung nicht abzusehen ist. Daher soll
über diese, die zumeist von DEWERRA ([dW97] [dW96]) gefunden wurden, lediglich eine tabellarische
Übersicht gegeben werden. Auf die ersten drei Fälle wird in Abschnitt 4.10 nochmals näher eingegangen
| Bezeichnung | Beschreibung |
| Perfekte Graphen | für jeden ind. Teilgraph gilt 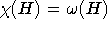 |
| Total unimodulare Graphen | Jede Submatrix der Adjazenzmatrix hat Determinante 0,1,-1 |
| Balancierte Graphen | Linegraphen von Bäumen |
| PROS-perfekte Graphen | Graphen, die unabhängig von gewissen Parametern ein halbpreemptives JSS erlauben |
| Candies, Crowns, Caterpillars | Spezialfälle von PROS-Perfekten Graphen |
| Ice-perfekte Graphen | Graphen, die eine Färbung erlauben, bei der die einzelnen Farben, die an einem Knoten anliegen, aufeinanderfolgen |
| BOC-Graphen | bipartiter Graph, der keine drei geraden Ketten enthält, die sich in ihren Endpunkten treffen |
(c) Martin Loehnertz 1999