Ablauf der Auktion und Strategien
Next: Erste Versuche einer Implementierung Up: Verfahren 2: Handels - Previous: Spieltheorie
Ablauf der Auktion und Strategien
Auktionsschemata
Eine erste Einschränkung der Möglichkeiten der Händler kann dadurch erzielt werden, daß ihnen ein bestimmtes
Handelsschema auferlegt wird, so daß beliebige Tauschoperationen nicht mehr möglich sind.
Im Verlauf der Zeit wurden zahllose Methoden entwickelt, Auktionen abzuhalten, um Ressourcen jedweder Art mit maximalem
Profit oder nach irgendwelchen Gerechtigkeitskriterien zu verteilen. Am günstigsten wäre es natürlich, im Rahmen
einer einzigen Auktion sofort für allumfassende Zufriedenheit zu sorgen. Dies ist aber im gegebenen Fall nicht möglich,
da sich die Wünsche der Teilnehmer mit Erwerb von Objekten ändern bzw. bei vorausschauender Berücksichtigung dieser Änderungen
das Auktionsschema eine Lösung des Gesamtproblems darstellen würde.
In der ökonomischen Literatur liegt ein wesentlicher Schwerpunkt beim Design von Auktionen auf Überlegungen, die
die Manipulierbarkeit des Marktes durch Händler betreffen, die besser über die Wünsche ihrer Konkurrenten informiert sind, als
diese über die ihren. Dies tritt natürlich im Rahmen einer Simulation nicht auf , so daß es kein Problem darstellt. Dennoch werden im folgenden Auktionsschemata
bevorzugt, bei denen diese Gefahr relativ gering wäre, da damit auch der probabilistische Anteil bei der
Strategiebestimmung umgangen werden kann. In der Sprache der Spieltheorie, die bezüglich Auktionen wesentlich
brauchbarere Ergebnisse liefert, heißt dies, daß die ehrliche Strategie jeweils dominant sein soll, d.h.
bei gleichem Verhalten der Gegner stets den anderen Strategien vorzuziehen ist.
, so daß es kein Problem darstellt. Dennoch werden im folgenden Auktionsschemata
bevorzugt, bei denen diese Gefahr relativ gering wäre, da damit auch der probabilistische Anteil bei der
Strategiebestimmung umgangen werden kann. In der Sprache der Spieltheorie, die bezüglich Auktionen wesentlich
brauchbarere Ergebnisse liefert, heißt dies, daß die ehrliche Strategie jeweils dominant sein soll, d.h.
bei gleichem Verhalten der Gegner stets den anderen Strategien vorzuziehen ist.
- Das einfachste Beispiel für eine solche Auktion ist Vickrey's Second Price Auction. Bei dieser Form gibt jeder Spieler sein Angebot geheim ab und der mit dem höchsten Angebot erhält das Objekt zum Preis des zweithöchsten Angebots. In [Bin92] wird gezeigt, daß das erwartete Ergebnis dieser Auktionsform mit dem der herkömmlichen Auktion übereinstimmt.
- Laut MIYAKE [Miy98] eine approximative Verallgemeinerung des obigen Vorgehens ist die Englische Auktion. Hier wird ein gemeinsames Preislevel für alle Beteiligten nach und nach angehoben, wobei die Teilnehmer jeweils angeben, ob sie noch weiter mitbieten. Ein Objekt zählt dann als zum momentanen Preis verkauft, wenn nur noch ein Käufer an ihm interessiert ist.
- Keine Auktion im eigentlichen Sinne, sondern mehr ein Verteilungsverfahren, das in einer gewissen Weise dem Heiratsalgorithmus [Sed92] ähnelt, ist das Verfahren von CRAWFORD und KNOER [CK81]. Ausgehend von einem Minimalpreis werden auch hier die Preise immer weiter angehoben. Ein Verkäufer kann sich temporär für einen Käufer entscheiden; dann bleibt dieser Preis stehen. Entscheidet er sich später um, so wächst dieser Preis von dem angegebenen Niveau aus weiter.
Aufgabenbereich der Händler und Strategiebestimmung
Durch die Komplexität gesetzte Grenzen
Da in die Überlegungen der Spieltheoretiker die Zeit, die zur Bestimmung der Strategien und zur Ermittlung eines Handelsprozesses notwendig ist, meist nur insofern einfließt, als überlegt wird, daß die entsprechenden Funktionen überhaupt (in endlicher Zeit) berechenbar sind, muß die Wahl einiger entscheidender Grundeigenschaften unter weitgehender Vernachlässigung dieses Kontextes getroffen werden.
Ist es, um die Existenz eines Equilibriums zu fördern, auch sinnvoll, die Zahl der Spieler sehr groß zu wählen, so setzt die Umsetzbarkeit der entsprechenden Handelsmechanismen hier harte Grenzen. Insgesamt sieht man sich mit der Situation konfrontiert, daß, bezeichnet man die Zahl der Spieler mit s, den Aufwand für die Strategiebestimmung mit a, die Zahl der benötigten Iterationen mit i, und die Komplexität des Handelsverfahrens mit h, sich der benötigte Gesamtaufwand ungefähr gemäß i(h(s)+as) verhält, während diese Werte untereinander in einem reziproken Wachstumsverhältnis stehen.
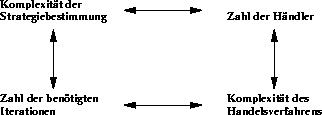
Hierbei muß allerdings beachtet werden, daß der Aufwand für das Handelsverfahren (h(s)) mit wachsender Händlerzahl ansteigt, auch wenn das Verfahren als solches einfacher wird.
Als erstes Problem bei einer Modellierung des Timetabling-Problems im Rahmen des oben dargestellten Kontextes stellt sich also die
Frage, was die Objekte sein sollen und wie sie auf die Händler zu verteilen sind. Will man hier nicht bestimmte Objekte den anderen vorziehen, so bietet es sich an,
jeder Gruppe einen Händler zu assoziieren, was der intuitiven Vorstellung Englisch in der 5 soll so
gut behandelt werden, wie Mathematik in der 7 wohl auch am nächsten kommt. Die ersten in dieser
Arbeit vorgenommenen Testimplementierungen folgten auch dieser Überlegung.
Es ist aber so, daß diese Methode
insbesondere was die betrachtete Realschule anbelangt, bei der viele Kurse nur aus einer einzelnen Stunde bestehen, zu einer
sehr großen Zahl von Händlern führt (ca. 300) . Z.B. das Verfahren von BACHEM, das zur Bestimmung des Trading Matchings\
Backtracking verwendet, kann mit einer so großen Zahl von Händlern nicht effizient implementiert werden. Einfachere Auktionsschemata hingegen können dies bewältigen.
Einfachere Auktionsschemata hingegen können dies bewältigen.
Das nächste Problem liegt in der Häufigkeit der Strategiebestimmung. Bei der Englischen Auktion und dem
Verfahren von [CK81] muß nach jeder Erhöhung des Preisniveaus jeder Händler seine Strategie von
neuem überdenken. Dies ist wiederum zu aufwendig, da auch bei diesem Verfahren nur bei hohen Iterationszahlen gute
Ergebnisse zu erwarten sind.
Mögliche Modelle
Wie bereits angedeutet besteht eine Möglichkeit darin, für jeden zu verteilenden Kurs einen Händler einzurichten, was insbesondere den Vorteil hat, daß er nur einen Typ von Gruppe erwerben muß und daher die Entscheidung entfällt, welche der erworbenen Ressourcen er welcher Gruppe zuordnen soll. Der damit sehr großen Zahl von Händlern muß entsprechend dadurch Rechnung getragen werden, daß z.B. ein einfaches Second-Price Auktionsmodell gewählt wird. Da dieses im Gegensatz zu den beiden anderen keine unmittelbare relative Preisentwicklung bietet, muß hier als Preis das jeweils beste Angebot der letzten Runde gewählt werden.
Im rein schulischen Kontext hingegen könnte eine Bevorzugung der Klassen sinnvoll sein, da der pädagogische Auftrag hier Vorrang vor den anderen Überlegungen hat. Zudem ist es so, daß die Klassen nahezu soviele Stunden Unterricht haben, wie für sie zur Verfügung stehen, so daß trotz des mit dem Zusammenfassen von Klassen verbundenen Sinkens der Händlerzahl die Komplexität der Strategiebestimmung nicht steigt, da nun nur die wenigen Stunden bestimmt werden müssen, an denen die Klasse frei hat. Ein Vorgang der in etwa der Tatsache entspricht, daß das Finden von sehr großen Cliquen in Graphen ähnlich einfacher ist wie das von solchen geringer Größe.
Strategiebestimmung
Die einfachste Form der Strategiebestimmung bestünde darin, keine Strategie zu verwenden, sondern die Händler ihr Guthaben je nach Wert auf alle Objekte verteilen zu lassen. Dies hätte aber den Nachteil, daß bei diesem Vorgehen der größte Teil des Geldes unberührt bliebe, da stets nur ein geringer Teil der möglichen Objekte erworben wird.
Zunächst scheint es sinnvoll zu sein, daß jeder Händler die beste Konfiguration erwerben will, die er für das
ihm zur Verfügung stehende Geld bekommen kann. Wie sich aber herausstellt, ist die Bestimmung dieser Menge bereits
wieder 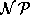 -hart. Würde man zunächst noch vermuten, daß das genaue Wissen um die benötigte Zahl der Objekte hier eine Hilfe wäre, so erkennt man doch, daß
sich das allgemeine Bin-Packing-Problem darauf reduzieren läßt, sofern man die gewünschte Anzahl frei, d.h. insbesondere
größer als die Zahl der Objekte in einem optimalen packing wählen kann:
-hart. Würde man zunächst noch vermuten, daß das genaue Wissen um die benötigte Zahl der Objekte hier eine Hilfe wäre, so erkennt man doch, daß
sich das allgemeine Bin-Packing-Problem darauf reduzieren läßt, sofern man die gewünschte Anzahl frei, d.h. insbesondere
größer als die Zahl der Objekte in einem optimalen packing wählen kann:
Dazu genügt es, bei diesem zu jeder
Paketgröße eine feste (große) Konstante zu addieren, sowie einige Hilfspakete hinzuzufügen, deren Größen genau dieser
Konstante entsprechen. Setzt man dann die neue Bin-Größe auf ein Vielfaches dieser Konstante zuzüglich der
alten Bin-Größe, so werden offenbar stets entsprechend viele Pakete verwandt, und diejenigen unter ihnen,
die keine Hilfspakete sind, stellen eine Lösung des Ausgangsproblemes dar. Dabei ist allerdings anzumerken, daß es für dieses Problem sowohl einen pseudopolynomiellen
Algorithmus, der auf dynamischer Programmierung beruht [Sed92], als auch polynomielle Approximationsschemata [Hoc97] gibt. Obwohl hier
im Schnitt nur drei oder vierelementige Mengen durch vollständiges Durchsuchen geprüft werden müssen, was im Prinzip in 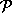 liegt, ist dies zu langwierig um entsprechend häufig durchgeführt zu werden.
liegt, ist dies zu langwierig um entsprechend häufig durchgeführt zu werden.
Eine erste Möglichkeit besteht darin, das verbleibende Budget gleichmäßig aufzuteilen, und die jeweils besten Objekte zu ermitteln, die einzeln diese Grenzen nicht überschreiten. Dies führt aber natürlich zu einer hohen Wechselrate bei den ausgewählten Gruppen.
Daher könnte nur eine Veränderung von je einem Zeitslot zugelassen werden. D.h jeder Händler kann pro Handelsrunde sein Interesse an einer Zeitstunde aufgeben und stattdessen für Objekte aus einer neuen Zeitstunde bieten. Diese einfache Form des Übergang erlaubt es zudem, bei der Wahl einer neuen Zeitstunde zu berücksichtigen, wieviel beim Verkauf einer passenden alten Stunde gewonnen werden kann. Im folgenden sei dieser Vorgang so er angewandt wird - damit bezeichnet, daß ein Händler die eine Zeitstunde zugunsten der anderen aufgibt. Hierbei muß allerdings darauf geachtet werden, daß der Händler auch die nichtveränderten Zeitstunden immer wieder prüft, da sich hier die Preise der dynamischen Objekte seiner Gruppen ändern können.
Zusätzlich tritt hier aber noch das Problem der flexiblen Ressourcen auf. Wie auch bei den Zeitstunden ist es
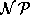 -hart, aus einem gegebenen Angebot die besten zu einem vorgegebenen Maximalpreis auszuwählen. Hier kann entweder
greedy nach dem besten Preis/Leistungsverhältnis vorgegangen werden oder aber wiederum eine feste
Obergrenze für jedes einzelne Objekt verwandt werden.
-hart, aus einem gegebenen Angebot die besten zu einem vorgegebenen Maximalpreis auszuwählen. Hier kann entweder
greedy nach dem besten Preis/Leistungsverhältnis vorgegangen werden oder aber wiederum eine feste
Obergrenze für jedes einzelne Objekt verwandt werden.
Erzwingen des Anhaltens
Auch wenn die Existenz eines Equilibriums nicht gesichert werden kann, so sollte es, in Anlehnung an die obigen
Überlegungen zu Homotopien, einen Punkt geben, an dem das Ganze anhält, so daß die Wahrscheinlichkeit vergrößert wird, daß bei Übergang
von einer Konfiguration zur nächsten nur wenige Schritte notwendig sind, um wieder in einen solchen Stundenplan zu gelangen.
Hierzu werden in der ersten Testimplementierung zwei Verfahren eingesetzt: Das erste Verfahren ist,vom Handelsverhalten her noch sinnvoll, daß
ein Händler ein Objekt, an dem er selbst noch interessiert ist, auf jeden Fall zu einem höheren Preis als
seinem Wert für ihn verkaufen muß. Würden die Agenten also nie ihre Wünsche ändern, würden die Preise
monoton steigen und die begrenzte Geldmenge würde irgendwann ein Anhalten erzwingen. Es muß also noch dafür
gesorgt werden, daß es nicht zu einem Kreisen in der Menge der von den Händlern angeforderten Zeitstunden kommt.
Hier hilft die folgende Beobachtung: Im Falle eines Kreisens müßte es stets vorkommen, daß ein Händler eine Zeitstunde
zugunsten einer anderen Zeitstunde aufgibt, zugunsten der er erstere bereits schon einmal aufgegeben hat.
Es erscheint im Sachkontext nicht vollkommen abwegig anzunehmen, daß er gelernt hat, daß ihm dies nichts bringt und
dies somit zu unterbinden. Da es nur endlich viele Zeitstunden gibt, die Menge aller geordneten Paare also
ebenfalls beschränkt ist, heißt dies, daß alle Händler nach einer endlichen Zahl von Schritten ihre Wunschzeitstunden
nicht mehr ändern könnten, woraufhin die obige Preispolitik zu einem Erliegen des Handels führen würde.
Bei den anderen Methoden der Strategiebestimmung läßt sich dieses Verfahren allerdings nicht anwenden. Hier könnte man
z.B. verlangen, daß jedes Objekt nur über seinem Einkaufspreis verkauft werden darf. Dies würde zwar ein Anhalten garantieren,
erscheint aber im Sachkontext nicht sinnvoll.
Kooperation und Wahl des Homotopie - Parameters
Zunächst würde es kanonisch erscheinen, den Geldwert in Abhängigkeit von der Zeit
sinken zu lassen. Da dieser aber für alle Spieler gleichmäßig sinken würde, würde der
Markt dies durch eine gleichmäßige Erhöhung aller Preise ausgleichen, so daß der
Effekt nur der wäre, daß Geschäfte ab einen bestimmten Umsatz aus Geldmangel
nicht mehr möglich sind.
Daher sollte der Zeitparameter derart in die individuellen Zielfunktionen der Spieler integriert werden, daß deren Wunsch nach vollständigen
Gruppen immer größer wird. Somit könnte man mit konvexen Zielfunktionen beginnen, die die Existenz eines
ersten Equilibriums sichern. Dies würde aber das System bereits ab einem sehr frühen Zeitpunkt erstarren lassen, da
beim Kauf eines Objektes sozusagen alle Objekte bezahlt werden müßten, die der Verkäufer in dieser Zeitstunde besitzt.
Daher könnte so vorgegangen werden, daß der Käufer einen festgelegten Anteil an den übrigen Besitztümern des Verkäufers erwirbt
und anteilhaft ausgezahlt wird, wenn diese verkauft werden. Im Verlauf des Handels wird dieser Anteil immer weiter
erhöht, bis am Ende stets der ganze Set bezahlt werden muß.
Diese Art der Verzerrung liefert aber noch kein einfaches Minimum für den Anfang. Um dies zu erreichen, werden die Objekte zu Beginn
von außen, d.h. von einem reinen Verkäufer und mit stetig sinkenden Preisen in den Markt eingeführt. Damit erhält man als triviales
Ausgangsequilibrium den Zustand, in dem keiner der Händler einen Gegenstand besitzt. Voraussetzung hierfür ist aber wiederum,
daß Geld als solches für die Händler einen Wert besitzt, da er ansonsten sein gesamtes Geld für den Ersterwerb ausgibt
und dieses somit für die Handelssituation verloren wäre.
Dies deckt sich insbesondere mit den Bedingungen von GALE [Gal84], der verlangt, daß kein Spieler
für irgendein Objekt sein gesamtes Geld ausgeben darf, und daß jeder Spieler eine Grenze hat, jenseits der er
nichts investiert.
Next: Erste Versuche einer Implementierung Up: Verfahren 2: Handels - Previous: Spieltheorie (c) Martin Loehnertz 1999