Direkte Heuristiken
Next: Wissensbasierte Verfahren / Expertensysteme Up: Lösungsansätze Previous: Lösungsansätze
Direkte Heuristiken
Die direkten Heuristiken sind zumeist unmittelbar aus den Erfahrungen der menschlichen Stundenplaner abgeleitet, wobei jedoch kaum mehr als allgemeine Vorgehensreihenfolgen gewonnen werden konnten. Die Verfahren basieren letztendlich alle auf einem Greedy-Verfahren mit Backtracking und wählen lediglich jeweils einen anderen Weg durch den Suchbaum, um einer Lösung möglichst nahe zu kommen, bevor zum erstenmal ein Schritt rückgängig gemacht werden muß.
Das folgende Lemma mag zwar auf den ersten Blick erfreulich erscheinen, aber das Bestimmen der als existent bewiesenen Reihenfolge ist offenbar wieder 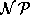 -vollständig:
-vollständig:
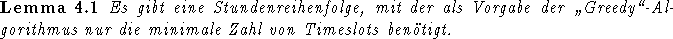
Beweis:
Es sei ein Stundenplan, der nur die minimal notwendige Stundenzahl benötigt, gegeben. Die gesuchte Reihenfolge ergibt sich,
indem man die einzelnen Timeslots in irgendeiner Reihenfolge - und auch intern jeweils beliebig - ausliest. Offenbar kann der Greedy-Algorithmus nur Stunden in
früher aufgeführte Zeitstunden verschieben, was die weitere Verteilung aber nicht stört.
Daher nun zu heuristisch inspirierten Wahlen von Reihenfolgen:
- Klassenreihenfolge: Dieses wohl einfachste Verfahren besteht darin, jeweils den Stundenplan für eine ganze Klasse festzulegen und dann zur nächsten überzugehen. Tritt eine Überlappung auf, werden entsprechend viele Schritte rückgängig gemacht. Der Vorteil gegenüber einer Lehrerreihenfolge besteht darin, daß Klassenspringstunden unerwünschter sind als Lehrerspringstunden.
- Scarcest Ressource first: Hier wird die Reihenfolge durch das Verhältnis von Angebot und Nachfrage nach den jeweiligen Ressourcen geregelt. Stunden, die stark nachgefragte Ressourcen verwenden, werden in der Hoffnung zuerst verplant, daß das Einsetzen der folgenden Stunden trotz der wachsenden Möglichkeiten einer Überschneidung erleichtert wird. Da sich Ressource hier durchaus auch auf Gruppen und Kombinationen von Ressourcen beziehen kann, ist die Bestimmung der seltensten zumeist nicht trivial, sondern erfordert das Wissen eines erfahrenen menschlichen Stundenplaners. In Programmen wird zumeist so vorgegangen, daß mehrere Planungsversuche unternommen werden und jeweils diejenigen Objekte, die die größten Schwierigkeiten bereiteten, im nächsten Durchlauf als die seltensten angenommen werden.
- Blockungen: Diese heute zumeist nur noch für die Gymnasiale Oberstufe eingesetzte Methode besteht darin, nichkollidierende Veranstaltungen zu einer Gruppe zusammenzufassen und diese dann als eine neue Veranstaltung zu behandeln. Vorteile dieses Vorgehens sind eine Reduktion der zu verplanenden Elemente und ein sehr regelmäßig strukturierter Stundenplan. Es existieren Programme, die ausschließlich zum Erstellen solcher Blöcke dienen, ohne daß konkrete Schulstunden betrachtet werden.
- Teile und Herrsche: Fast zwangsläufig wird häufig versucht, das Problem in mehrere Teilprobleme zu zerlegen. Dies ist insbesondere möglich, wenn man ohnehin einige Objekte vorbehaltlos bevorzugen möchte. Z.B. wird häufig der Plan für die gymnasiale Oberstufe ohne Rücksicht auf den noch zu erstellenden Mittelstufenplan festgelegt.
Next: Wissensbasierte Verfahren / Expertensysteme Up: Lösungsansätze Previous: Lösungsansätze (c) Martin Loehnertz 1999