Der Normalfall
Next: Zusammenfassung Up: Komplexität des Problems Previous: Die Komplexität von Teilproblemen
Der Normalfall
All diese Überlegungen zeigen, daß es nach dem derzeitigen Stand der Dinge aus informatischer Sicht eigentlich nahezu unmöglich sein müßte, einen geeigneten Stundenplan zu erzeugen. Dennoch kann jede Schule einen solchen vorweisen. Dies legt nahe, daß es in der Realität irgendwelche noch nicht erfaßte Randbedingungen gibt, die das Problem wesentlich vereinfachen. Untersuchungen dieser Art gibt es z.B. für das Vehicle Routing Problem . Dort konnte gezeigt werden, daß die Eckpunkte
des zugehörigen Polyeders der möglichen Lösungen überdurchschnittlich häufig ganzzahlig sind [RF88].
Bei der automatische Stundenplanerstellung ist auffällig, daß die Aufgabenstellung zumeist aus der nach [CK95b] ebenfalls
nur mit exponentiellem Aufwand zu bestimmenden Lehrerverteilung hervorgeht, wenn auch,
wie auch von diesen Autoren betont, deren Integration in das Gesamtproblem eleganter wäre.
. Dort konnte gezeigt werden, daß die Eckpunkte
des zugehörigen Polyeders der möglichen Lösungen überdurchschnittlich häufig ganzzahlig sind [RF88].
Bei der automatische Stundenplanerstellung ist auffällig, daß die Aufgabenstellung zumeist aus der nach [CK95b] ebenfalls
nur mit exponentiellem Aufwand zu bestimmenden Lehrerverteilung hervorgeht, wenn auch,
wie auch von diesen Autoren betont, deren Integration in das Gesamtproblem eleganter wäre.Hinzu kommt, daß in der schulischen Praxis ein Stundenplan kein isoliertes Problem, sondern eine Problemabfolge ist: Es ist relativ einfach, zu einem gegebenen Stundenplan für die Klassen Lehrer so (neu) einzustellen, daß der Plan erfüllt werden kann: Es genügt bei ähnlichen Curricula, z.B. alle Klassen die Fächer in derselben Reihenfolge durchnehmen zu lassen, diese aber jeweils um 1 gegeneinander zu verschieben. D.h. sozusagen, der erste Stundenplan, den eine Schule benötigt, ist einfach zu erstellen. Beim Übergang von einem Jahr zum nächsten ändern sich strukturell meist nur wenige Dinge, da die Jahrgangsgrößen in Klassenzahlen selten um mehr als
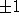 schwanken und nur ein Jahrgang ausgewechselt wird. Zudem bleiben die Curricula zumeist gleich.
schwanken und nur ein Jahrgang ausgewechselt wird. Zudem bleiben die Curricula zumeist gleich.
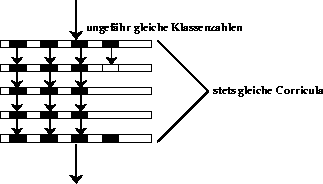
Die Frage hier wäre also, ob die Lösbarkeit des letztjährigen Stundenplanproblems hinreichend ist für die Existenz eines neuen Stundenplans.
Beim Hinzunehmen der Gymnasialen Oberstufe verschwindet dieser Effekt allerdings teilweise, da hier die
individuellen Wahlen der Schüler den Plan in starkem Maße verändern können.
Auch scheint es so, daß die Prüfungsverteilung (vgl. Kapitel 2.6), bei der solche Regelmäßigkeiten noch seltener
auftreten, in der Praxis schwieriger ist.
Next: Zusammenfassung Up: Komplexität des Problems Previous: Die Komplexität von Teilproblemen (c) Martin Loehnertz 1999