Die Komplexität von Teilproblemen
Next: Der Normalfall Up: Komplexität des Problems Previous: Randomisierte Algorithmen/Heuristiken
Die Komplexität von Teilproblemen
Insbesondere im Rahmen eines interaktiven Systems ist die Komplexität von Teilproblemen interessant, da seitens des Benutzers häufig verlangt wird, lokale Widersprüche aufzuheben. Im folgenden wird daher immer ein Teil des Problems bzw. ein bestimmter Parameter als konstant angenommen.
Festhalten des Zeitpunkts
Geht es lediglich darum, die zu einem bestimmten Zeitpunkt angeforderten Ressourcen zu verteilen, so kann dies
durch einfaches Matching geschehen: Siehe Abschnitt 8.4.3.
Abhängigkeiten zwischen flexiblen Ressourcen - wie z.B. Bevorzugung von benachbarten Klassenräumen - können aber bereits nicht mehr in polynomieller Zeit aufgelöst werden.
Es gibt auch keinen approximativen Algorithmus, da dieses Problem durch Komplementbildung in das der maximalen unabhängigen Teilmenge überführt werden kann.
Sei ein Graph gegeben, in dem eine Clique gegebener Größe u zu finden ist: Assoziiert man jeden
Knoten mit einer flexiblen Ressource und legt die Vorlieben so fest, daß zwei Ressourcen einander
bevorzugen wenn die entsprechenden Kanten verbunden sind, so korrespondiert offenbar eine entsprechende
Clique im Graphen zu einer optimalen Ressourcenzuteilung von u Objekten.
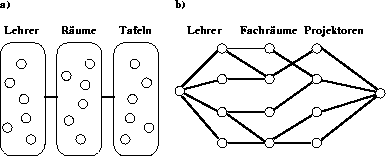
Kann man die Objekte aber nach Wichtigkeit der Wünsche so aufteilen, daß die jeweiligen Gruppen innerhalb keine
Abhängigkeiten aufweisen, so besteht auf jeder Ebene nur das Problem, die u bevorzugtesten Elemente auszuwählen (a). Sind
diese zusätzlich nur von einigen Elementen der höheren Ebene abhängig, läßt sich das Ganze durch Netzwerkflüsse behandeln (b)
.
Das oben angesprochene Matching wird dann ein Spezialfall dieses Verfahrens mit zwei Ebenen:
Allerdings zeigt dieses Teilproblem ein Verhalten, das dem von 2SAT bzw. von Max2SAT ähnelt: Ist eine
Menge von Stunden gegeben, der Ressourcen zugeteilt werden sollen, bei der aber nicht gesichert ist, daß wirklich
jede Stunde mit Räumen o.ä. versorgt werden kann, so ist das Problem, eine optimale Lösung zu finden,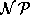 
- hart und
nicht konstant approximierbar. Denn: Gegeben ein Graph, in dem eine maximale unabhängige Menge gefunden werden soll,
assoziiere jeden Knoten mit einer Stunde, füge für jede Kante einen gesonderten Raum hinzu, und stelle die Anforderung,
daß die beiden inzidenten Stunden genau diesen Raum brauchen. Offenbar korrespondiert dann eine maximale
Zahl verteilter Stunden zu einer maximalen unabhängigen Knotenmenge.
Während das Entscheidungsproblem also in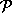 
liegt, ist das Optimierungsproblem sehr schwer.
Eine ebenfalls 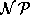-harte Variante ergibt sich, wenn man verlangt, daß zu allen Zeiten die gleichen Ressourcen, z.B. Räume, verwandt werden sollen.
Hier erhält man wieder ein allgemeines Graphenfärbungsproblem, indem man die Räume als Farben und die Veranstaltungen als Knoten
interpretiert, die genau dann verbunden sind, wenn sich diese zu irgendeinem Zeitpunkt überschneiden.
Festhalten eines Objekts
Wie [dW85] zeigt, kann auch unter der Annahme von Abwesenheitszeiten der Plan für eine einzelne Klasse optimal durch Netzwerkflüsse gelöst werden.
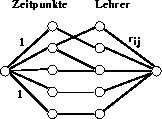
Das gleiche kann natürlich auch für Lehrer, Räume etc. durchgeführt werden.
Festhalten der Blockungen
Hat man die Schulstunden den Zeitstunden zugeordnet, so läßt das Permutieren der Zeitstunden die Gültigkeit der harten Nebenbedingungen unberührt. Betrachtet man hier zunächst nur die indirekten Nebenbedingungen, so erhält man in der einfachsten Form - nur Relationen zwischen aufeinanderfolgenden Stunden - eine Variante des Problems des Handlungsreisenden. Will man z.B. den Wochenplan einer Klasse unter dem Aspekt modifizieren, daß die zurückzulegende Wegstrecke minimiert wird, so erhält man eventuell noch eine euklidische Metrik, so daß Approximationsalgorithmen wie der von ARORA [Vyg] anwendbar bleiben. Kommen dazu noch Regelungen wie die, daß auf eine Schwimmstunde z.B. nicht Mathematik folgen sollte, so müssen die Entfernungen in diesem Problem noch nicht einmal mehr der Dreiecksungleichung genügen, was dazu führt, daß noch nicht einmal eine Approximation bis auf einen konstanten Faktor möglich ist [Jun90]. Es können zudem natürlich auch mehrere Stunden übergreifende Relationen auftreten.
Next: Der Normalfall Up: Komplexität des Problems Previous: Randomisierte Algorithmen/Heuristiken (c) Martin Loehnertz 1999