Approximierbarkeit

Fälle mit unbeschränktem Grad

Minimierung der Zeitstundenzahl
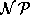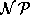Bei zahlreichen -vollständigen Problemen kann sowohl die Approximation bis auf konstante Abweichung, als auch bis auf einen gewissen konstanten Faktor als ebenfalls -vollständig nachgewiesen werden. Es zeigt sich, daß bei uneingeschränkten Formen von Prüfungsverteilungen und beim University-Timetabling noch wesentlich schlechtere Verhältnisse vorliegen, da das Problem des Graphenfärbens darauf L-reduziert werden kann.

Das heißt, wenn es einen Approximationsalgorithmus für B gibt, gibt es auch einen für A, wobei dieser höchstens um einen konstanten Faktor schlechter ist. Im folgenden soll gezeigt werden, daß - wenn man keine speziellen Voraussetzungen anwendet - ein approximativer Algorithmus für das Timetabling-Problem verwendet werden könnte, um das Färben eines Graphen zu approximieren.

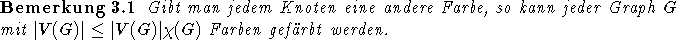
In [Hal93] wird - allerdings basierend auf anderen Voraussetzungen - die Vermutung geäußert, daß keine bessere Approximation als 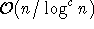für ein festes c möglich ist. Die Reduktionen auf die beiden genannten TimetablingProbleme erweisen sich als triviale Umformungen, die, da jeweils eins zu eins Beziehungen zwischen den zu färbenden Objekten bestehen, offensichtlich L-Reduktionen sind: Für jeden Knoten wird ein Termin vorgesehen und für jede Kante eine Person, die an beiden Terminen teilnimmt.

Es kann natürlich dennoch approximative Algorithmen für bestimmte Spezialfälle geben. Die Anforderungen an einen solchen wären relativ zu der obigen Aussage aber recht hoch, da z.B. herkömmliche Schul-Stundenpläne bei 40 zur Verfügung stehenden Wochenstunden Klassen bis zu 30 Unterrichtsstunden in der Woche haben können, so daß mit 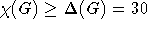mindestens ein 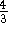- Approximationsalgorithmus gefunden werden müßte, wobei es unwahrscheinlich ist, daß tatsächlich eine Färbung mit 30 Farben existiert.

Vorgegebene Zeitstundenzahl
Man kann die Anforderung an einen Timetabling-Algorithmus also zu präzisieren versuchen und fragen, ob es einen Algorithmus gibt, der, gegeben eine Zahl k von Farben, einen Graphen mit diesen färbt und nur einen konstanten Anteil der Knoten ungefärbt läßt. Aber auch hierfür ergibt sich, daß der allgemeine Fall unlösbar ist:

Beweis:
Man wendet den Algorithmus mit stets neuen k Farben iteriert auf die jeweils noch nicht gefärbten Knoten an. Dies muß man höchstens 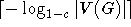mal anwenden, bis weniger als 1 Knoten übrig ist.

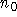Für jedes gibt es aber ein , so daß 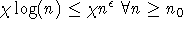ist wobei anzumerken ist, daß es zu jedem k beliebig große Graphen G mi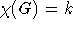t gibt.

Um diesen Fall zu betrachten, kann des weiteren folgende Konstruktion herangezogen werden ([Tuz97],[dW95]): Jeder Knoten des Graphen werde durch eine Clique der Größe k ersetzt, wobei mit jedem Knoten der Clique eine Farbe assoziiert wird. Die neuen Knoten seien jeweils durch das Paar aus alter Knotenbezeichnung und Farbe markiert. Dann verbindet man alle Knoten gleicher assoziierter Farbe miteinander, deren Originale im Ausgangsgraphen verbunden waren. Die Kantenmenge des neuen Graphen ergäbe sich somit also als

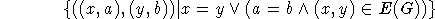
Offenbar korrespondiert eine unabhängige Menge im neuen Graphen zu einer korrekten, aber nicht notwendig vollständigen Färbung des alten, wenn man ein Element dieser Menge so interpretiert, daß der Originalknoten eines ausgewählten Knotens die diesem assoziierte Farbe erhält. Die Wohldefiniertheit wird hierbei durch die Cliquen und die Korrektheit durch die übrigen Kanten gewährleistet.
Diese Konstruktion erlaubt es zudem, einige relative Nebenbedingungen zu modellieren, da man nun dafür sorgen kann, daß Zuordnungen einander ausschließen. So z.B. kann man jede Kombination (s,x), bei der s eine Schwimmstunde für die entsprechende Klasse darstellt, mit allen Stunden (p,y) verbinden, bei denen p eine Mathematikstunde derselben Klasse und y eine Stunde ist, die am selben Tag aber später als x liegt. Damit wäre dann sichergestellt, daß niemals Mathematik auf Schwimmen folgen kann.
Umgekehrt kann man natürlich das Problem der maximalen unabhängigen Teilmenge (MIS) als das Problem ansehen, einen Graphen mit k=1 Farbe so zu färben, daß möglichst wenige Knoten übrigbleiben. [Hoc97] folgend ist dieses Problem im nicht gradbeschränkten Fall konsistent damit genauso hart wie das des Graphenfärbens, da auch für das MIS eine untere Approximierbarkeitsschranke des selben Typs angegeben werden kann [Has96].
Ein Vorteil, den man gegenüber dem allgemeinen Graphenfärbungsproblem hat, ist, daß, da der Graph aus einem anderen Problem konstruiert wurde, die Cliquenzahl bekannt ist, deren Ermittlung normalerweise ebenfalls hart ist. Hieraus läßt sich aber für einen exakten Algorithmus anscheinend kein Vorteil gewinnen, da, obwohl z.B. in einem planaren Graphen alle Cliquen in 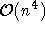aufgezählt werden können, die Entscheidung ob dieser 3- oder 4-färbbar ist, 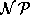-vollständig ist. Ob dies die Approximation erleichtert, scheint bisher noch nicht untersucht worden zu sein. Zudem ist mit der Lovaszschen 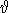-Funktion [Knu94] stets ein Wert bekannt, der zwischen chromatischer Zahl und Cliquenzahl liegt, so daß somit eine bessere untere Schranke für 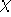immer gegeben ist.

Insgesamt läßt sich also sagen, daß das Problem, wenn man keine Anforderungen an die Größe der Differenzierungen stellt, nicht mit konstanter Qualität approximierbar ist.

Beschränkter Grad

Minimierung der Zeitstundenzahl
Für den Fall, daß man die Größe der Differenzierungsgruppen als beschränkt annimmt, funktioniert die obige Reduktion des Knotenfärbens nicht mehr, da das Timetablingdann zu Fällen mit begrenztem Knotengrad korrespondiert. Die umgekehrte Transformation ist natürlich auch möglich, was dazu führt, daß der Satz von Brooks, der 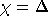zeigt [Die96], anwendbar wird. Dies liefert aber dennoch keinen Algorithmus für die automatische Stundenplanerstellung, da der Knotengrad hier im Schnitt ca. dreimal größer ist, als die angestrebte Farbenzahl. Selbst dann wäre er nur um 1 besser, als die von jedem Greedy-Algorithmus garantierbare Schranke von .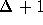
Relaxiert man die Ansprüche weiter und verlangt, daß nur ein bestimmter Anteil der Kanten beide Enden in der jeweils gleichen Farbklasse hat, so gelangt man zum Begriff der sogenannten Semifärbungen, wobei bei diesen ein Fehleranteil von maximal 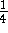vorgesehen ist. Hier läßt sich mit hoher Wahrscheinlichkeit und unter Einsatz semidefiniter Programmierung eine Semi-Färbung mit 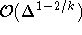Farben erzielen [Hoc97], was selbst, wenn man als Konstante nur 1 zuläßt, mit 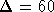und k=30 zu einer Farbenzahl von 52 führen würde, wobei wegen der relativ großen Zahl von Kanten noch immer jeder Knoten mit einer ungültigen Kante inzident sein könnte. 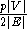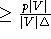Nach dem Schubfachprinzip müßte, um einen Anteil von p gesetzten Stunden zu garantieren, die Approximationsgüte bezüglich der Kanten 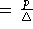betragen.

Vorgegebene Zeitstundenzahl
Wählt man die selbe Reduktion auf das MIS-Problem wie im letzten Abschnitt, so liegt auch hier der Fall mit beschränktem Grad vor, da die Größe jeder Clique durch k und die Zahl der übrigen Kanten durch den (beschränkten) Grad des Originalknotens gegeben ist. Für Graphen mit 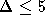zeigen BERMAN und KARPINSKI [BK98], daß sich eine Approximationsgüte von 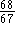nicht unterschreiten läßt. Dies wäre zwar noch hinreichend, aber die erreichbare Güte scheint mit wachsendem Grad strikt größer zu werden.
Betrachtet man die entsprechenden Approximationsversuche für das Problem der maximalen unabhängigen Knotenmenge in gradbeschränkten Graphen, so findet sich beispielsweise in [BF96] eine Approximationsgüte in der Größenordnung von 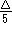, was in diesem Fall bedeuten würde, daß nur ca. 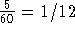der Knoten gefärbt würde ,wobei die hier eingesetzten Zahlwerte, die voraussetzen, daß es nur Differenzierungen der Größe 3 mit je 20 Stunden pro Objekt gibt, meiner Ansicht nach mehr als optimistisch sind. Durch die umgekehrte Reduktion und durch die Anwendung des Satzes von Brooks erhielte man . Unter der Voraussetzung, daß für den zu färbenden Graphen 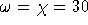gilt, erhielte man durch iteriertes Färben mit 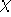Kanten also 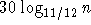, was nur für 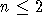zu weniger als 38 Farben führt.
Das Problem mit beschränktem Grad ist somit zwar konstant approximierbar, aber die Qualität ist für die praktische Anwendung nicht ausreichend. Polynomielle Approximationsschemata existieren für diesen Fall - zumindest in dieser Allgemeinheit - ebenfalls nicht, was diese Variante des Problems in die Komplexitätsklasse APX-PB, die laut [KMSV94] mit dem Abschluß der formalen Klasse MAX SNP übereinstimmt, einordnet.

Gewichtete Fälle

Da man stets eine Gewichtung mit den Werten 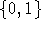wählen kann, sind die gewichteten Problemstellungen mindestens so schwer wie die ungewichteten. Über die exakte Komplexität und Approximierbarkeit des allgemeinen Falles gibt die Literatur soweit mir bekannt keinerlei Auskunft. Das Problem liegt natürlich in 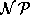, da es möglich ist, all diese Kriterien in polynomieller Zeit zu überprüfen. Läßt man die die relativen Nebenbedingungen gänzlich außer Acht, so gelangt man zum GOCCP, über dessen allgemeine Approximierbarkeit nichts bekannt ist, das aber auf speziellen Graphenklassen gelöst werden kann (s. Abschnitt 4.10.1).
Verwendet man hier - eine vorgegebene Farbenzahl vorausgesetzt - erneut die obige Konstruktion zum Übergang auf das MIS-Problem an, so gibt es in [Hoc97] ein anwendbaren Approximationsalgorithmus, der eine minimale unabhängige Kantenmenge mit einem Gewicht findet, das vom optimalen nur um 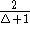abweicht. Dieses Verfahren besteht im wesentlichen in der Ausnutzung einer vorangegangenen Zerlegung des Graphen in Farbklassen. 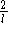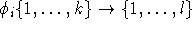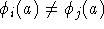Könnte das obige Suchproblem besser gelöst werden und eine Färbung mit l Farben gefunden werden, so kann dies sogar auf verbessert werden, da man aus einer Färbung des Ausgangsgraphen stets eine Färbung des neuen (MIS-) Graphen erhalten kann, indem man l injektive Abbildungen mit 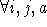wählt, was z.B. durch zyklisches Permutieren geht. Dann ordnet man dem Knoten (a,b) die Farbe 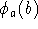zu. In praktischen Anwendungen ist es natürlich dennoch nicht sinnvoll, diese Färbung, die, wenn man die kleinsten l-k der Farbklassen als nichtgefärbt deklariert, immerhin 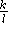approximativ war, zugunsten einer gewichteten 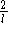-Approximation aufzugeben.